When doing frequency synthesis with fractional-N PLLs, one often needs to find a rational approximation of a floating point number with the constraint that the numerator must not be larger than a certain number. The more exact the approximation is, the closer the actual frequency will be to the desired one.
The integer part is obviously easy, but the fractional part requires a more sophisticated algorithm. One such algorithm is based on Farey sequences and the formula for finding the next fraction between two Farey neighbors.
The Farey sequence of order N consists of all completely reduced fractions between 0 and 1. So e.g. the Farey sequence of order 3 consists of {0/1, 1/3, 1/2, 2/3, 1/1}. A sequence of a higher order contains all the terms of all lower orders and then some more. So, with a fractional-N PLL where the denominator is limited to some value D, the possible fractional parts of the N in the PLL is precisely the fractions present in the Farey sequency of order D. And our goal is to find the best one to approximate the fractional part of the desired N, i.e. a number between 0 and 1.
There is a neat and useful formula for finding the next fraction that will appear between two Farey neighbors as the order of the sequence is increased. If a/b < c/d are neighbors in some Farey sequence, the next term to appear between them is the mediant (a+c)/(b+d). So an algorithm to find better and better rational approximations to a number x is to
- Start with the Farey sequence of order 1, i.e. {0/1, 1/1}, where a/b = 0/1 and c/d = 1/1 are neighbors.
- Calculate the mediant (a+c)/(b+d) = (0+1)/(1+1) = 1/2.
- Figure out which of a/b and c/d are further from x than the mediant and replace it with the mediant.
- Go to 2 if the denominator is not yet larger than what is allowed.
- Use the best result previous to the denominator becoming too large.
This algorithm is described on this archived web page.
This seems fine, until one considers some special cases. Say e.g. the target number is 0.000 001 and the maximum allowed denominator is 2 000 000. The algorithm would narrow down the top end of the interval from 1/1 to 1/2 to 1/3 to 1/4… in each successive iteration. It would thus take a million steps before the perfect approximation of 1/1 000 000 is reached. This is hardly efficient in this case, even though it converges quickly in many (most) other cases.
A way to speed up these degenerate cases is to not just take a single step in each iteration, but instead figure out how many times in a row either a/b or c/d will be discarded in favor of the mediant. It turns out that this is not too hard to do.
If e.g. a/b is to be discarded K times in a row, the resulting number will be (a + K*c)/(b + K*d). So how many times K will a/b be discarded until it is time to narrow down the interval from the other end? Set (a + K*c)/(b + K*d) = x and solve for K, which gives K = (x*b – a)/(c – x*d). K is often not an integer, so then select the biggest integer smaller than K.
If it is instead c/d that is to be discarded, the formula for K is (c – x*d)/(x*b – a).
With this improvement, it takes just one step to get to 1/1 000 000 instead of a million. Quite an improvement.
But there is still a minor numerical issue. When a decimal number can be perfectly expressed as a fraction, a calculation for K might end up very close to, but still less than 1, even though the perfect answer would be 1 exactly. This means that the floor function will return 0 instead of 1 and we might get stuck in an infinite loop where zero is added to the numerator and denominator, so nothing changes. To resolve this, a very tiny positive value should be added before calling the floor() function. There are 53 bits in the mantissa of doubles, so a number slightly larger than one would have an LSB representing 2-52 ≈ 2.2 *10-16. There may be further rounding errors in the calculations, so the tiny value should be well above this level to ensure K does not erroneously end up just below 1. I discovered this problem when trying to approximate 0.288 = 36/125.
I wrote some C-code to implement this improved algorithm. Here it is:
// Farey sequence-based rational approximation of numbers.
// Per Magnusson, 2024, 2025
// MIT licence, http://www.opensource.org/licenses/mit-license.php
#include <cstdint>
#include <cmath>
// Type to represent (positive) rational numbers
typedef struct {
uint32_t numerator;
uint32_t denominator;
uint32_t iterations; // Just for debugging
} rational_t;
// Find the best rational approximation to a number between 0 and 1.
//
// target - a number between 0 and 1 (inclusive)
// maxdenom - the maximum allowed denominator
//
// The algorithm is based on Farey sequences/fractions. See
// https://web.archive.org/web/20181119092100/https://nrich.maths.org/6596
// a, b, c, d notation from
// https://en.wikipedia.org/wiki/Farey_sequence is used here (not
// from the above reference). I.e. narrow the interval between a/b
// and c/d by splitting it using the mediant (a+c)/(b+d) until we are
// close enough with either endpoint, or we have a denominator that is
// bigger than what is allowed.
// Start with the interval 0 to 1 (i.e. 0/1 to 1/1).
// A simple implementation of just calculating the mediant (a+c)/(b+d) and
// iterating with the mediant replacing the worst value of a/b and c/d is very
// inefficient in cases where the target is close to a rational number
// with a small denominator, like e.g. when approximating 10^-6.
// The straightforward algorithm would need about 10^6 iterations as it
// would try all of 1/1, 1/2, 1/3, 1/4, 1/5 etc. To resolve this slow
// convergence, at each step, it is calculated how many times the
// interval will need to be narrowed from the same side and all those
// steps are taken at once.
rational_t rational_approximation(double target, uint32_t maxdenom)
{
rational_t retval;
double mediant; // float does not have enough resolution
// to deal with single-digit differences
// between numbers above 10^8.
double N, Ndenom, Ndenom_min;
uint32_t a = 0, b = 1, c = 1, d = 1, ac, bd, Nint;
const int maxIter = 100;
if(target > 1) {
// Invalid
retval.numerator = 1;
retval.denominator = 1;
return retval;
}
if(target < 0) {
// Invalid
retval.numerator = 0;
retval.denominator = 1;
return retval;
}
if(maxdenom < 1) {
maxdenom = 1;
}
mediant = 0;
Ndenom_min = 1/((double) 10*maxdenom);
int ii = 0;
// Farey approximation loop
while(1) {
ac = a+c;
bd = b+d;
if(bd > maxdenom || ii > maxIter) {
// The denominator has become too big, or too many iterations.
// Select the best of a/b and c/d.
if(target - a/(double)b < c/(double)d - target) {
ac = a;
bd = b;
} else {
ac = c;
bd = d;
}
break;
}
ii++;
mediant = ac/(double)bd;
if(target < mediant) {
// Discard c/d since the mediant is closer to the target.
// How many times in a row should we do that?
// N = (c - target*d)/(target*b - a), but need to check for division by zero
Ndenom = target * (double)b - (double)a;
if(Ndenom < Ndenom_min) {
// Division by zero, or close to it!
// This means that a/b is a very good approximation
// as we would need to update the c/d side a
// very large number of times to get closer.
// Use a/b and exit the loop.
ac = a;
bd = b;
break;
}
N = (c - target * (double)d)/Ndenom;
Nint = floor(N);
if(Nint < 1) {
// Nint should be at least 1, a rounding error may cause N to be just less than that
Nint = 1;
}
// Check if the denominator will become too large
if(d + Nint*b > maxdenom) {
// Limit N, as the denominator would otherwise become too large
N = (maxdenom - d)/(double)b;
Nint = floor(N);
}
// Fast forward to a good c/d.
c = c + Nint*a;
d = d + Nint*b;
} else {
// Discard a/b since the mediant is closer to the target.
// How many times in a row should we do that?
// N = (target*b - a)/(c - target*d), but need to check for division by zero
Ndenom = (double)c - target * (double)d;
if(Ndenom < Ndenom_min) {
// Division by zero, or close to it!
// This means that c/d is a very good approximation
// as we would need to update the a/b side a
// very large number of times to get closer.
// Use c/d and exit the loop.
ac = c;
bd = d;
break;
}
N = (target * (double)b - a)/Ndenom;
Nint = floor(N);
if(Nint < 1) {
// Nint should be at least 1, a rounding error may cause N to be just less than that
Nint = 1;
}
// Check if the denominator will become too large
if(b + Nint*d > maxdenom) {
// Limit N, as the denominator would otherwise become too large
N = (maxdenom - b)/(double)d;
Nint = floor(N);
}
// Fast forward to a good a/b.
a = a + Nint*c;
b = b + Nint*d;
}
}
retval.numerator = ac;
retval.denominator = bd;
retval.iterations = ii;
return retval;
}
To test the algorithm on an Arduino (actually a Pi Pico), I wrote the following code:
#include <arduino.h>
typedef struct {
double target;
uint32_t maxdenom;
uint32_t expected_numerator;
uint32_t expected_denominator;
uint32_t maxiter;
} rational_test_case_t;
void test_rational_approx()
{
rational_t result;
rational_test_case_t test[] = {
{0, 3000, 0, 1, 2},
{1, 3000, 1, 1, 2},
{0.5, 3000, 1, 2, 2},
{0.5+1/3001.0, 3000, 751, 1501, 5},
{1/3001.0, 2500, 1, 2500, 2},
{1/3001.0, 1500, 0, 1, 2},
{1/3001.0, 3001, 1, 3001, 2},
{0.472757439, 1816, 564, 1193, 10},
{0.472757439, 1817, 859, 1817, 10},
{0.288, 100000000, 36, 125, 10},
{0.47195, 1048575, 9439, 20000, 12},
{0.471951, 1048575, 471951, 1000000, 15},
{1/128.0, 1048575, 1, 128, 2},
{17/65536.0, 1048575, 17, 65536, 3},
{0.618033988749895, 1000000, 514229, 832040, 30}, // Golden ratio - 1, worst case in terms of number of iterations
{0.141592653589793, 56, 1, 7, 2},
{0.141592653589793, 57, 8, 57, 2},
{0.141592653589793, 106, 15, 106, 3},
{0.141592653589793, 113, 16, 113, 4},
{0.141592653589793, 32000, 4527, 31972, 5},
{0.141592653589793, 32989, 4671, 32989, 5},
};
uint32_t n_tests = sizeof(test)/sizeof(test[0]);
for(uint32_t ii = 0; ii < n_tests; ii++) {
result = rational_approximation(test[ii].target, test[ii].maxdenom);
Serial.printf("target = %.8g, maxdenom = %lu, ", test[ii].target, test[ii].maxdenom);
Serial.printf("approx = %lu/%lu, iter = %lu ", result.numerator, result.denominator, result.iterations);
if(result.numerator == test[ii].expected_numerator &&
result.denominator == test[ii].expected_denominator &&
result.iterations <= test[ii].maxiter) {
Serial.println(" OK");
} else {
if(result.iterations > test[ii].maxiter) {
Serial.printf("Too many iterations (max %lu) ", test[ii].maxiter);
}
Serial.printf("Expected %lu/%lu\n", test[ii].expected_numerator, test[ii].expected_denominator);
}
}
}
The printout from the code is:
target = 0, maxdenom = 3000, approx = 0/1, iter = 0 OK
target = 1, maxdenom = 3000, approx = 1/1, iter = 0 OK
target = 0.5, maxdenom = 3000, approx = 1/2, iter = 1 OK
target = 0.500333222, maxdenom = 3000, approx = 751/1501, iter = 4 OK
target = 0.000333222259, maxdenom = 2500, approx = 1/2500, iter = 1 OK
target = 0.000333222259, maxdenom = 1500, approx = 0/1, iter = 1 OK
target = 0.000333222259, maxdenom = 3001, approx = 1/3001, iter = 1 OK
target = 0.472757439, maxdenom = 1816, approx = 564/1193, iter = 7 OK
target = 0.472757439, maxdenom = 1817, approx = 859/1817, iter = 8 OK
target = 0.288, maxdenom = 100000000, approx = 36/125, iter = 5 OK
target = 0.47195, maxdenom = 1048575, approx = 9439/20000, iter = 11 OK
target = 0.471951, maxdenom = 1048575, approx = 471951/1000000, iter = 14 OK
target = 0.0078125, maxdenom = 1048575, approx = 1/128, iter = 1 OK
target = 0.000259399414, maxdenom = 1048575, approx = 17/65536, iter = 2 OK
target = 0.618033989, maxdenom = 1000000, approx = 514229/832040, iter = 28 OK
target = 0.141592654, maxdenom = 56, approx = 1/7, iter = 2 OK
target = 0.141592654, maxdenom = 57, approx = 8/57, iter = 2 OK
target = 0.141592654, maxdenom = 106, approx = 15/106, iter = 2 OK
target = 0.141592654, maxdenom = 113, approx = 16/113, iter = 3 OK
target = 0.141592654, maxdenom = 32000, approx = 4527/31972, iter = 4 OK
target = 0.141592654, maxdenom = 32989, approx = 4671/32989, iter = 4 OKI also implemented the algorithm in an Excel sheet:
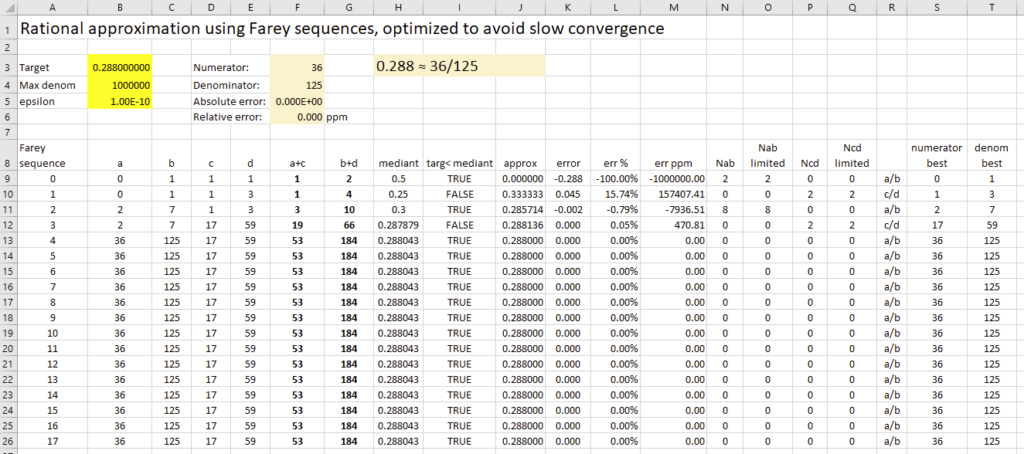
The excel document is available here:
Hi Per, Thank you for posting this
I am using your code for a si5351a project and did some testing with 100k random real targets (between 0 and 1) for generating a numerator/denominator and comparing that real result to the original requested real for error.
That was interesting as most of the time (with max denom = 1048575) the resulting num/denom, when calculated as a double, had small error relative to the original requested target
The histogram was heavily centered on small error. Not a bell curve though.
There were outlier cases with larger errors. Surprising.
I compared your results to another “fast” Farey algorihm, which got similar results. So that was good. I think it’s not specific to your algo but inherent with the max denominator of 1048575. I ran another algo that targeted a max error, and it was able to reduce the error with a larger denominator. So I guess it’s just a question of the density of answers is not uniform across the space 0->1.
I changed your max iterations to 100 because I saw one case hitting the 1000 iteration limit. Seemed like it wasn’t improving with the large number of iterations.
Example case:
Here is one intereting case where it went to my 100 iteration limit..and got a higher error.
You can see the initial “Farey target” of 0.47195
surprising that was difficult?
for:
Farey target 0.47195000000000
I got this using your code and limit 1048575 (due to the 20-bit si5351a limit)
Farey numerator 6116
Farey denominator 12959
Farey iterations 101
Farey actual real 0.47194999614168
Farey actual real error 0.00000000385832
Do you agree with this result? I am curious if it’s inherent in the algorithm, or whether something in your code could be tweaked to improve this case.
thanks
Kevin
Hi Kevin,
Thanks for testing the code and reporting the issue. The Excel sheet does not have the same problem and it turns out that it all came down to a rounding issue. I had tried to work around it by adding “epsilon” before doing floor() when calculating how many steps to narrow the gap from either side. Despite this, the case you found caused N + epsilon to still be just below 1, so floor() of that value became 0 and the abcd values were not updated during that iteration or any of the following. The iteration counter eventually became too large and an earlier result was returned.
I have now updated the code and removed “epsilon”. Instead, I check if Nint is 0 and if so, force it to be 1. I hope this does not introduce any other problems, but it seems like it should be safe to do.
I also added your test case to the test code. It failed before I updated the algorithm, but now it passes. I also added a check to see that the algoritm did not use too many iterations.
Let me know if you find other cases where the result is incorrect.
Regarding the distribution of rational numbers of a maximum denominator (i.e. the numbers in a certain Farey sequence), you are correct that it is far from uniform if you look closely. The worst spots are near numbers with small denominators. The smaller the denominator, the bigger the gap to the nearest rational number. So at 0 and 1, the nearest neighbor is obviously off by 1/maxdenom. It does not get worse than that. At 1/2, the nearest numbers are off by approximately 1/(2*maxdenom). Generally, near a number A/B (with a small B), the nearest neighbors are at a distance of roughly 1/(B*maxdenom).
Again, thanks for pointing out the issue so I could fix it!
Per
This has been a very helpful post. Thank you for sharing.
I think you might find this interesting:
Today I was looking for other ways of converting floating point numbers to fractions. I learned about continued fractions and followed instructions to write an algorithm based on them. To reduce floating point error, I came up with a formula to calculate each partial denominator. I was quite surprised to end up with K = (x*b – a)/(c – x*d).
After a bit of debugging I realised that the flow of the continued fraction algorithm is the same as the flow of your optimized Farey sequence algorithm. The continued fraction method doesn’t keep track of a lower bound and upper bound, instead it keeps track of the result of the previous two iterations of the algorithm. The only significant difference between algorithms is that the initial “upper bound” is 1/0 instead of 1/1.
It felt like an appropriate conclusion that both strategies, despite beginning completely differently, converged on the same solution.