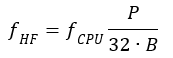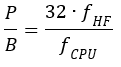En resa mot krångligare mjukvara för att
med minimalistisk hårdvara få fina RF-egenskaper

Den här artikeln publicerades först i QTC nummer 1 2025.

Programkod, filer för kretskortstillverkning och 3D-modeller för den färdiga sändaren finns på https://github.com/per-magnusson/RP2350-Foxoring-Transmitter. Texten här i del 1 beskriver hur mjukvaran fungerar och utvecklades mot att generera allt bättre radiosignaler direkt från pinnar på processorn.

Foxoring är en variant av rävjakt/radiopejlorientering där man använder väldigt svaga sändare som bara hörs inom en radie av 100 m eller så. För att hitta fram till pejlbart avstånd från sändaren är den ungefärliga positionen inritad på kartan, så man orienterar sig fram till närheten av sändaren och pejlar sig fram sista biten. Foxoring är inte så vanligt i Sverige och förekommer varken på de nationella tävlingarna eller på något SM. Inte heller finns grenen med på NM, men väl på EM och VM, så kanske borde vi i Sverige köra foxoringträningar och -tävlingar lite oftare?

Personligen gillar jag grenen dels för att jag som i grunden är orienterare har en fördel av att jag behärskar orienteringsmomentet som är mer uttalat i denna tävlingsform än i vanlig rävjakt, dels för att de svaga signalerna sätter mottagaren på prov och gör att man har mer att vinna på att utveckla känsligare mottagare. För vanlig rävjakt på 80m-bandet är det inget större problem att bygga en tillräckligt lågbrusig mottagare och göra antennen tillräckligt känslig, men på just foxoring ger varje dB extra signal/brusförhållande en liten extra fördel eftersom man då kan höra sändaren på längre avstånd och tidigare styra in mot den.

För att testa mina egenbyggda mottagare satte jag för länge sedan ihop en enkel sändare där en Si5351 (ganska billig PLL/klockgenerator som är populär i amatörradiosammanhang) sköter både frekvenssyntes och agerar (svagt) slutsteg. Med en 3 m lång antenn hörs den på åtminstone 500 m avstånd. Så att använda en sådan, ihop med en processor som konfigurerar den och sköter morsesändandet, som grund för en foxoringsändare är en uppenbar möjlighet.

Via Peder Haugaard Pedersen, SM0GNS, fick jag dock tips om ett sätt att använda en Raspberry Pi Pico, alltså en litet kort med en mikrokontroller, att självständigt skapa signaler i 80m-bandet helt utan behov av en extern PLL eller oscillator. Färdiga kort med processorn RP2040 (och den nyare RP2350), USB-kontakt, minne och spänningsregulator kostar ca 70–80 kr, så det borde gå att konstruera en enkel, lättbyggd och billig foxoringsändare med ett sådant kort som bas. Och med väsentligt mycket lägre strömförbrukning än om man dessutom behöver en separat Si5351. Processorerna går att programmera i mikro-python samt C/C++ via t.ex. Arduinomiljön. Själv använder jag oftast det senare.

RP2040 och RP2350 har ett par unika och kraftfulla inbyggda periferienheter som kallas PIO (programmable input/output) och som är nyckeln till att dessa processorer går att använda som HF-generatorer. PIO-modulerna är en sorts enkla processorer som man kan programmera i ett begränsat assemblerspråk.

PIO med frekvensdelare

Peders lösning bygger på ett PIO-program med två instruktioner, lägg en utgång hög och lägg den sedan låg (och hoppa tillbaka till början). En praktisk funktion i PIO:n är att återhoppet till början av programmet kan ske utan att det tar någon extra tid, så programmet skapar alltså en symmetrisk fyrkantsvåg. Det lilla PIO-programmet ser ut så här:

.wrap_target
   set   pins, 1   ; Set output high
   set   pins, 0   ; Set output low
.wrap

På [1] finns en online-assemblator för PIO-program som omvandlar dem till C-kod som man kan inkludera i sitt C-program för att konfigurera PIO:n på önskat sätt.

En finess i varje PIO är att man kan skapa dess klocka genom att dela ned processorklockan. Neddelningsfaktorn kan vara ett bråktal med åtta bråktalsbitar, så man kan alltså skapa klockfrekvenser (åtminstone i medeltal) som är processorklockan delat med ett tal på formen N + A/256 där N och A är heltal. En vanlig processorklockfrekvens är 133 MHz, men det går bra att överklocka processorn till exempelvis 150, 200 eller till och med 275 MHz (fast utan garanti att det fungerar). 200 MHz verkar ganska säkert, men 275 kanske inte fungerar helt robust på alla exemplar. Högre frekvens resulterar också i högre strömförbrukning. Den trots allt begränsade upplösningen på bråktalsdelarna gör att om man önskar en viss frekvens i bandet mellan 3,5 och 3,6 MHz så får man ett fel på maximalt ca 750 Hz vid 133 MHz processorfrekvens och max ca 500 Hz fel när man utgår från 200 MHz. Ofta hamnar man närmare. Det här är egentligen gott och väl tillräckligt bra för ändamålet eftersom det inte finns några förutbestämda kanalfrekvenser man måste hålla sig till vid rävjakt, utan kan välja en som går att realisera.

När man inte ska sända (mellan morsepipen) kan man antingen stoppa PIO:n eller vända riktningen på pinnen till en ingång så att ingen signal kommer ut.

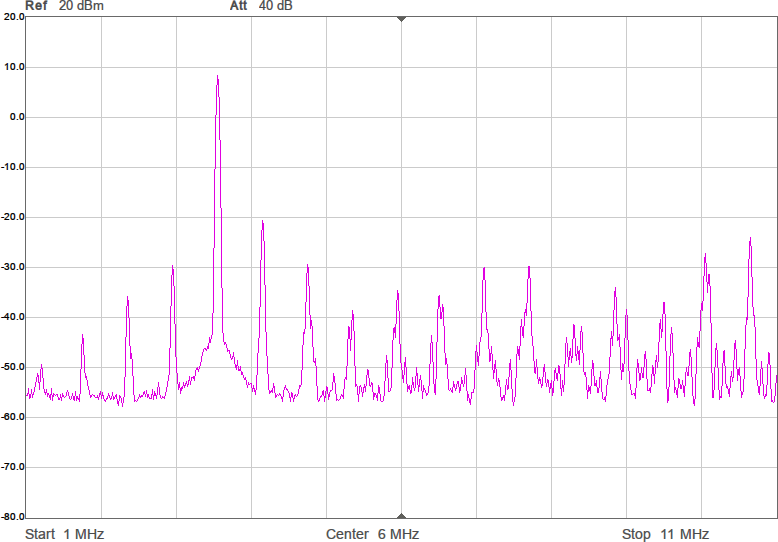
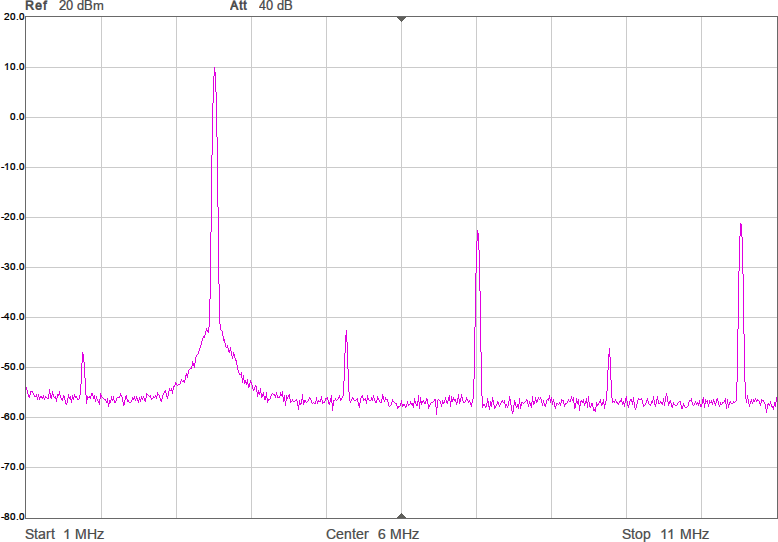
Utöver de harmoniska övertonerna vid multiplar av grundfrekvensen uppstår oftast en mängd spurioser i spektrumet eftersom bråktalsdelaren hoppar mellan olika heltal för att i medeltal hamna rätt. Exakt var spurioserna hamnar och hur starka de blir är olika för olika delarvärden. Figur 2a-d visar spektrum för några olika sändarfrekvenser vid 200 MHz processorklocka. De två renaste spektrumen har delare som är 28,5 respektive 28,0. Grundtonen är den högsta toppen medan tredje övertonen, HD3, ligger nära högra kanten. Andra övertonen, HD2, är bara signifikant i första spektrumet där delaren är 28,5.

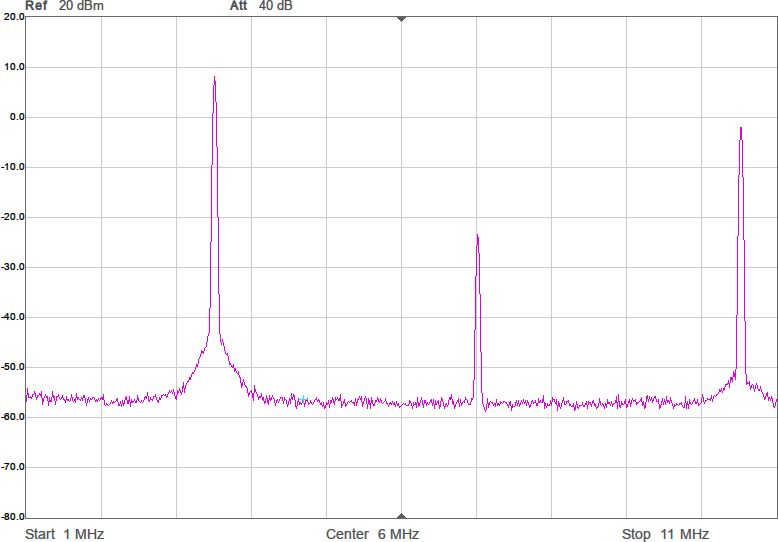
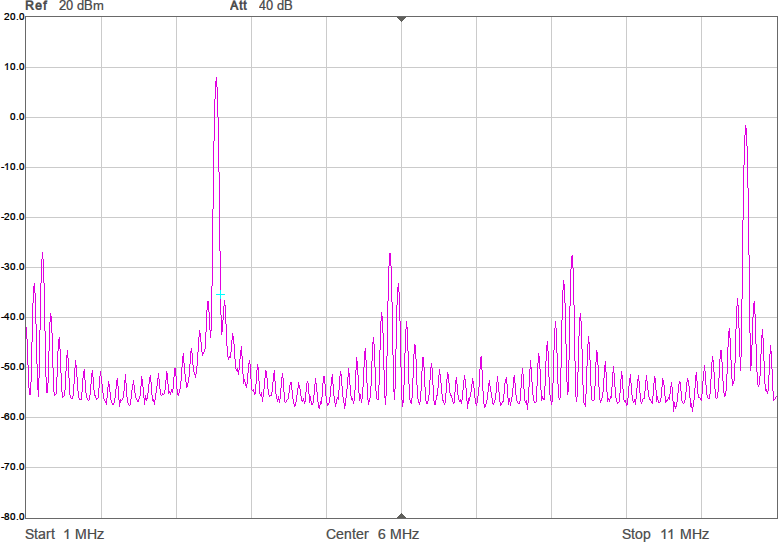
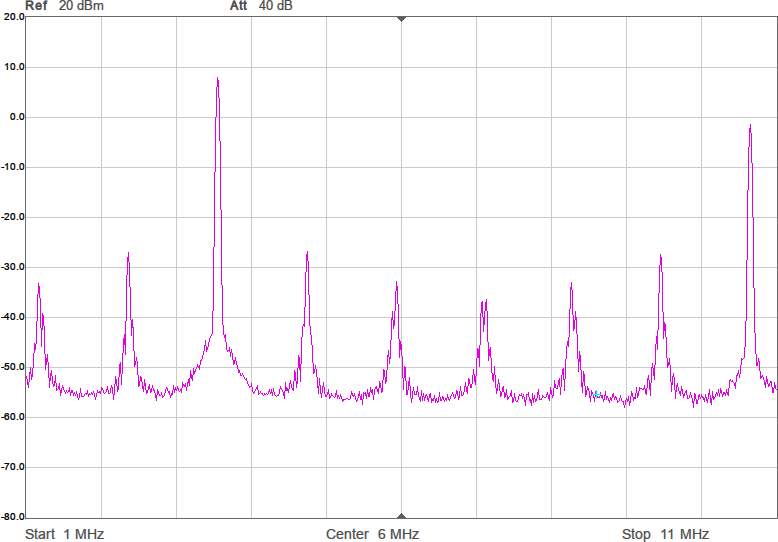
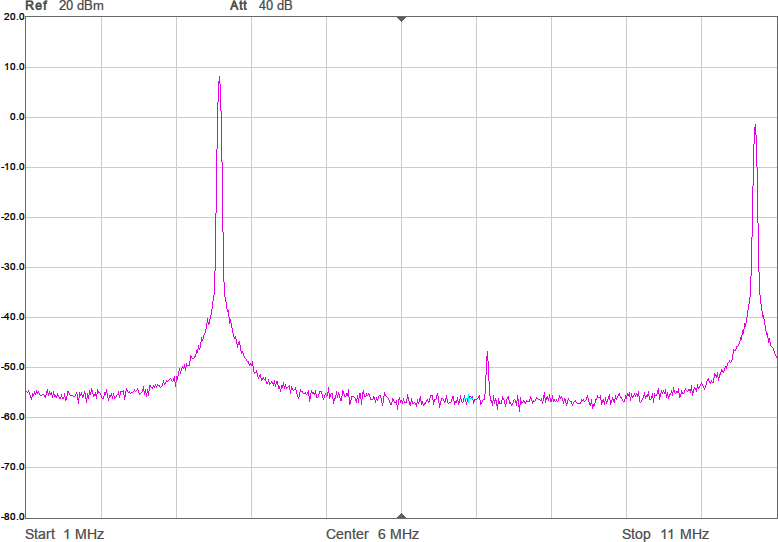
För att få en komplett sändare behövs ytterligare några detaljer:

• Ett lågpass- eller bandpassfilter som tvättar bort övertonerna (speciellt den vid tre gånger grundfrekvensen som i sig själv bara är ca 9 dB svagare än grundtonen eftersom det handlar om en fyrkantsvåg),
• en anpassning mot den nästan skrattretande korta antennen (30 cm är inte mycket att komma med på 80m-bandet),
• ytterligare lite programkod för att sända önskad morsekod och kanske lyssna på några knappar som väljer frekvens, rävnummer och morsetakt,
• tre AA-batterier eller en LiPo-cell för att driva det hela och
• en liten låda för väderskydd.

Ungefär här kunde artikeln vara slut, men jag hade ett par idéer om förbättringar som sedan började föröka sig…

Förbättringar som rör mjukvaran gör ju inte sändaren svårare eller dyrare att bygga, bara utvecklingstiden för programvaran längre och programkoden krångligare. Så låt oss se om det finns något att göra på främst mjukvarusidan.

Förberäknad vågform

Efter lite googlande hittade jag [2] som är en mer komplett sändare byggd runt en RP2040. Den klarar AM, FM och SSB, delvis tack vare en extern modulator. Med små förändringar i koden skulle den även klara CW. En idé i denna lösning som jag gillade var att den använder en PIO på ett annat sätt. Istället för att ha ett PIO-program som autonomt växlar mellan etta och nolla på en utgång så matar huvudprogrammet i processorn ettor och nollor till PIO:n som sedan skickas ut i full fart. PIO:n har nämligen ett FIFO-minne på åtta ord om 32 bitar som kan fyllas på från processorn. På utgången av FIFO:t finns ett 32-bitars skiftregister och det finns en praktisk PIO-assemblerinstruktion som tar en bit från skiftregistret och skickar ut på en av processorns pinnar. När skiftregistret är tomt laddas det med ett nytt ord från FIFO:t. Se Figur 3.

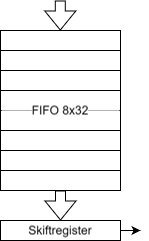
Det nya och väldigt korta PIO-programmet ser ut så här:

.wrap_target
   out   pins, 1  ; Shift out one bit
.wrap

Även detta program loopar hela tiden, så varje klockcykel körs instruktionen som skiftar ut en bit från skiftregistret till en pinne.

Via DMA (direct memory access) kan man fylla på med data i FIFO:t när det finns plats ledigt utan att alls belasta själva huvudprocessorn. Så genom att i förväg räkna ut hur en fyrkantsvåg ska se ut för att skapa önskad frekvens, lägga fyrkantsvågen på något ställe i minnet och sätta upp DMA och PIO så att datat i denna minnesbuffert upprepat pumpas ut till PIO:n i den takt det förbrukas så skapar man alltså en fyrkantsvåg med önskad frekvens. I detta fall kör man PIO:n med fulla processorklockan.

Vad är då fördelen med detta över den första och betydligt enklare lösningen som inte involverade några minnesbuffertar och DMA? Det blir väl en fyrkantsvåg i båda fallen med ungefär önskad frekvens? Jo, en poäng här är att man kan approximera önskad frekvens mer noggrant. Det man måste göra för att uppnå det är att välja längden på minnesbufferten smart. Den består av 32-bitarsord och innehållet i ett ord förbrukas alltså under 32 processorklockcykler. Eftersom samma sekvens spelas upp om och om igen är det viktigt att bufferten innehåller ett helt antal perioder av vågformen man vill skapa så att man inte får ett fult fashopp när man börjar om från början av bufferten. Antalet 32-bitarsord i bufferten är en fri parameter, så beroende på vilken frekvens man vill sända så kan man välja en lämplig buffertlängd för att det ska gå jämnt upp med ett heltal perioder i vågformen.

Om f_CPU är processorfrekvensen, f_HF är önskad bärvågsfrekvens, B är antalet 32-bitarsord i bufferten och P är antal perioder av vågformen som bufferten innehåller vill man alltså att B och P ska uppfylla:

Eller:

RP2040 har ganska mycket minne för att vara en mikrokontroller, 264 kB, dvs över 65 000 st 32-bitarsord. Om vi begränsar oss till exempelvis 10 000 ord i bufferten kan B alltså vara ett tal mellan 1 och 10 000. För varje B finns ett P som gör att vi hamnar närmast den f_HF vi vill ha med just det valet av B och för något B hamnar vi närmast av alla. Det vore lätt att gå igenom alla B, räkna ut bästa P och komma ihåg den hittills bästa kombinationen av B och P. Med ”bara” 10 000 som största värde på B går det dessutom ganska fort. Men varför göra det enkelt när man kan göra det bättre? I samband med att jag skrev mjukvara till mina pejlmottagare där en Si5351 används som lokaloscillator stötte jag på ett liknande problem där motsvarigheten till B är över en miljon vilket gör att testande av alla kombinationer skulle ta opraktiskt lång tid. Så då utvecklade jag en algoritm som mycket snabbare hittar fram till bästa bråktalsapproximation av ett tal när nämnaren är begränsad. Den bygger på något som kallas för Farey-sekvenser och den intresserade kan läsa mer detaljer om hur det fungerar på min blogg [3]. Denna färdiga lösning kan man återanvända även här för att snabbt hitta bästa P och B givet f_CPU, maximalt B och önskad f_HF.

Med tekniken att pumpa ut data från en färdiguträknad buffert som är upp till 10 000 ord lång får man en betydligt finare frekvensupplösning. De möjliga delningsfaktorerna är inte likformigt fördelade och det visar sig att det finns ett par specialfall där maximala felet för frekvenser mellan 3,5 och 3,6 MHz är ca 45 Hz om man klockar processorn med 200 MHz, men i de allra flesta fall blir frekvensfelet mycket mindre än 1 Hz. För multiplar av 1 kHz blir felet 0 Hz. Man använder då som mest B = 6250 ord, vilket ger f_HF = P∙1000 Hz. Om man nöjer sig med multiplar av 10 kHz kan man minska buffertlängden till 625 ord utan att få något avrundningsfel. Toleransen hos processorns kristall snarare än själva syntesmetoden avgör därmed noggrannheten i den skapade frekvensen.

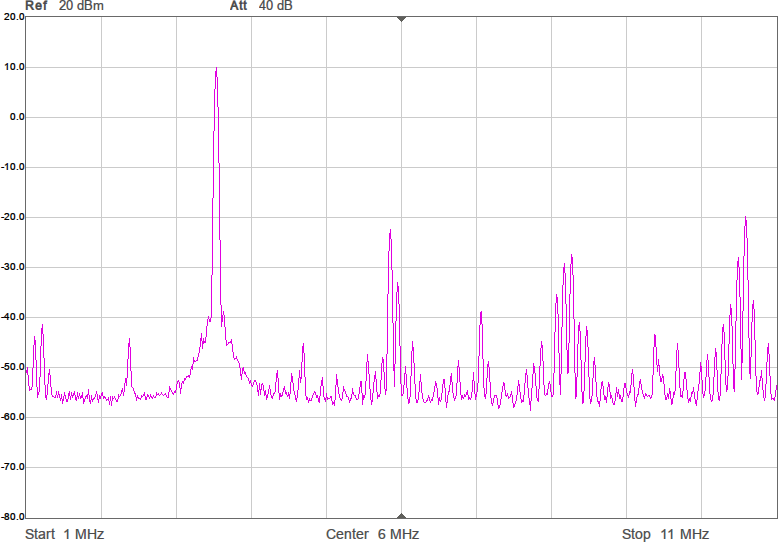
Figur 4 visar hur några spektrum blir med denna metod. Målfrekvenserna är desamma som i Figur 2. Som synes är det inte någon större skillnad på spektrumen jämfört med den tidigare metoden, vilket är förväntat eftersom det i båda fallen handlar om rena fyrkantsvågor som bara kan byta nivå var femte nanosekund (eftersom klockfrekvensen är 200 MHz).

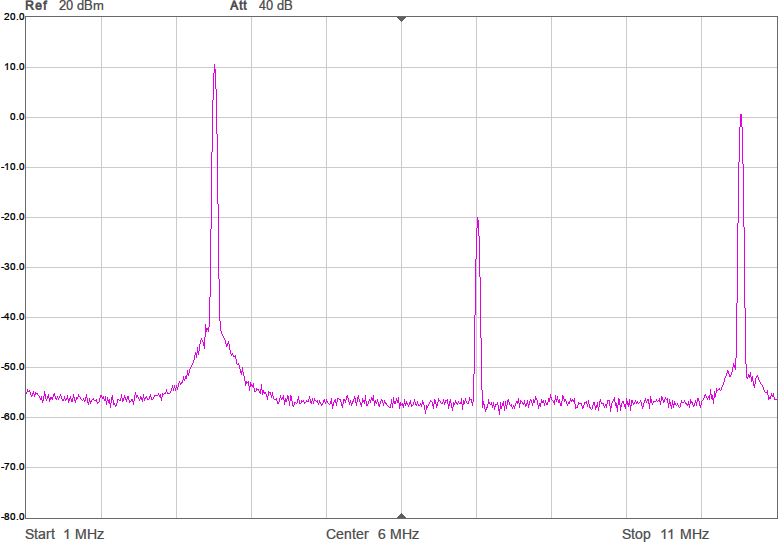
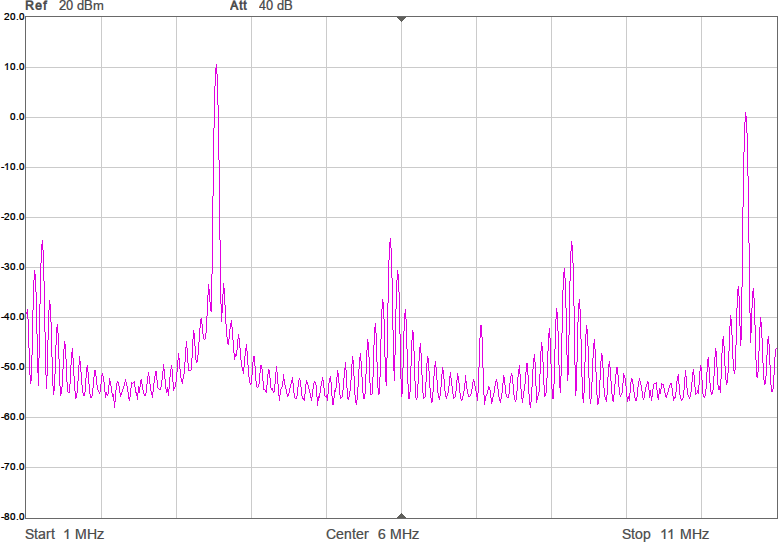
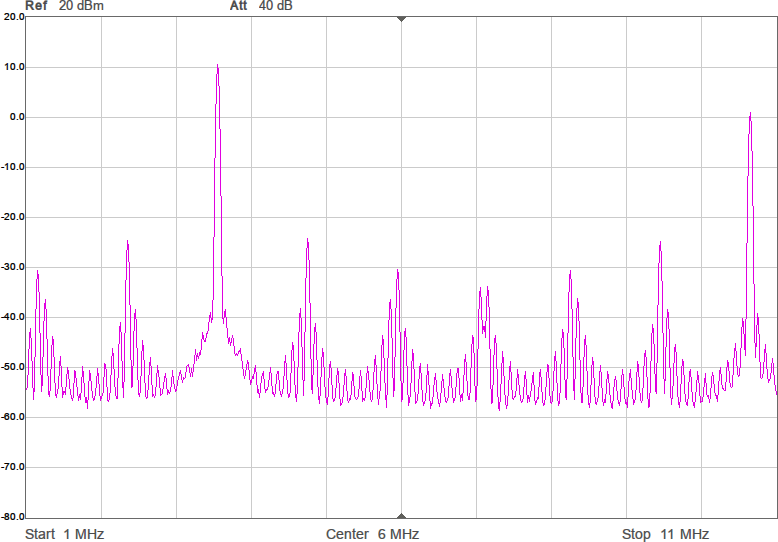
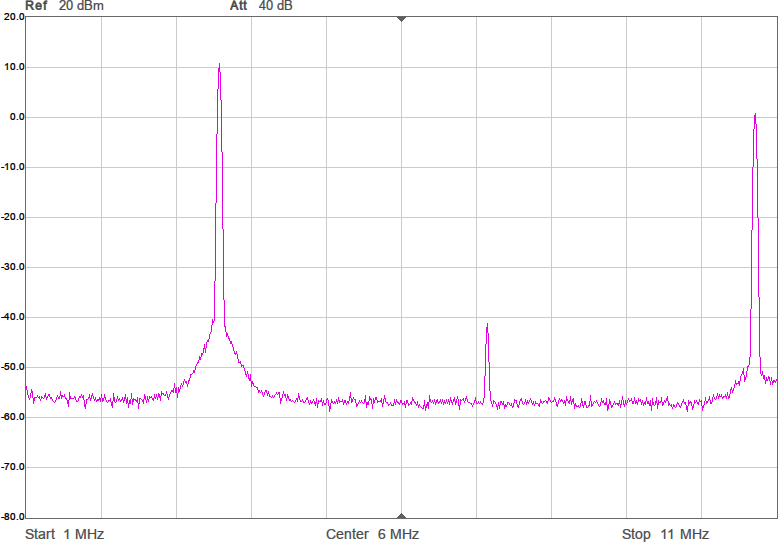
Inte så viktig förbättring kanske, men det är lite trevligt att ha större frihet att välja frekvens. Man skulle också kunna använda denna frihet för att kompensera för toleransen hos klockkristallen hos processorn om man gillar att finlira med sådant och bemödar sig att mäta upp verklig frekvens vid den temperatur som sändaren ska arbeta i. Den stora vinningen visar sig dock vara själva metoden att pumpa ut förberäknad data i full processorklocktakt till en pinne på processorn, för vi kan göra mer med denna metod.

Sigma-delta

När vågformen är beräknad i förväg kan vi lämna enkla fyrkantsvågor och ge oss in på något mer kraftfullt och lite mer komplicerat. Sigma-delta-modulering används ofta i audiosammanhang för att med ganska enkel och mestadels digital hårdvara skapa analog-till-digital (AD) och digital-till-analog (DA) -omvandlare med mycket hög upplösning och dynamik; ofta 24 bitar eller mer.

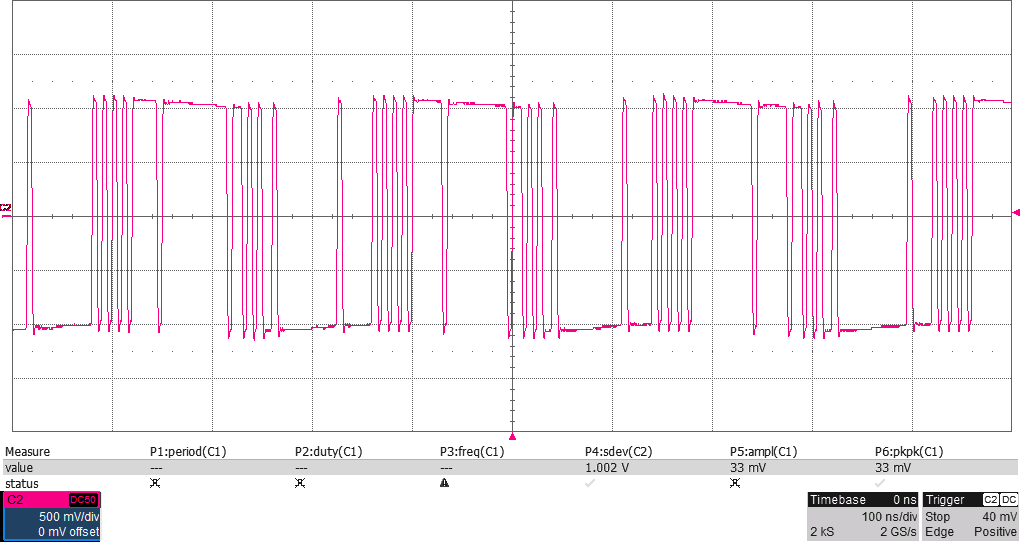
Principen för en sigma-delta DA-omvandlare bygger på att man håller reda på felet som skapas när man trösklar vågformen (t.ex. när man avgör om sinuskurvan ligger över eller under nollstrecket och väljer om utgången ska vara hög eller låg) och tar med det i beräkningen när man vid nästa klockcykel åter ska bestämma om utgången ska vara hög eller låg. För att resultatet ska bli bra krävs att klocktakten är många gånger högre än den frekvens man vill skapa. Resultatet är att utgången hoppar snabbt mellan hög och låg när vågformen man försöker efterlikna är nära noll, medan den ligger mer stabilt hög eller låg när vågformen är nära en topp eller dal. Figur 5 visar hur det kan se ut.

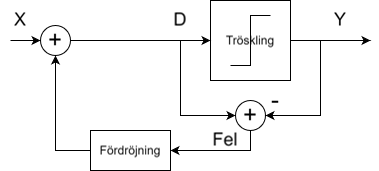
I Figur 6 visas hur blockschemat för moduleringen ser ut. Signalen man vill modulera (sinusvågen) kommer in från vänster vid X. Det tidigare felet adderas och resultatet D trösklas för att skapa utsignalen Y. Skillnaden mellan D och Y, dvs det fel som uppstår vid trösklingen, räknas ut och påförs insignalen vid nästa klockcykel.

Ser man på det spektralt visar det sig att sigma-delta-moduleringen gör att kvantiseringsbruset trycks upp till högre frekvenser och därmed blir lättare att filtrera bort. Man eliminerar också mycket av de harmoniska övertonerna. En ren fyrkantsvåg har en överton vid tre gånger grundfrekvensen (HD3) som är endast 9 dB lägre än grundtonen, men med sigma-delta-modulering kan den tryckas ned betydligt och minska kraven på det analoga filtret före antennen.

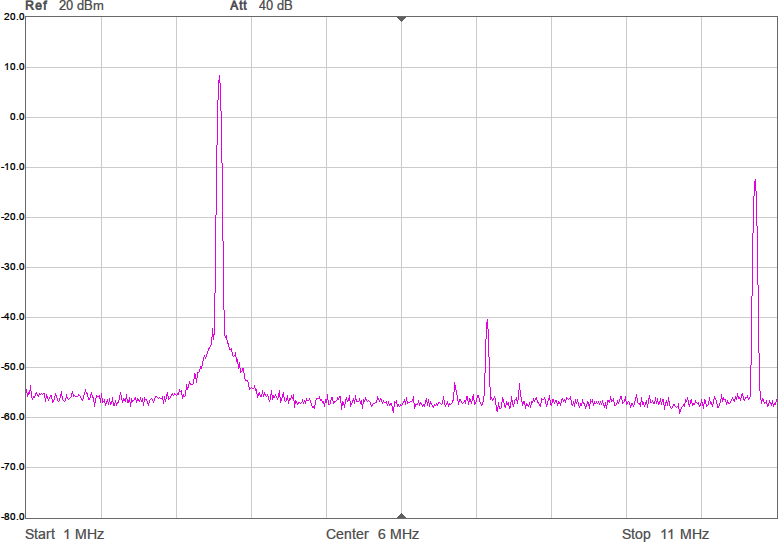
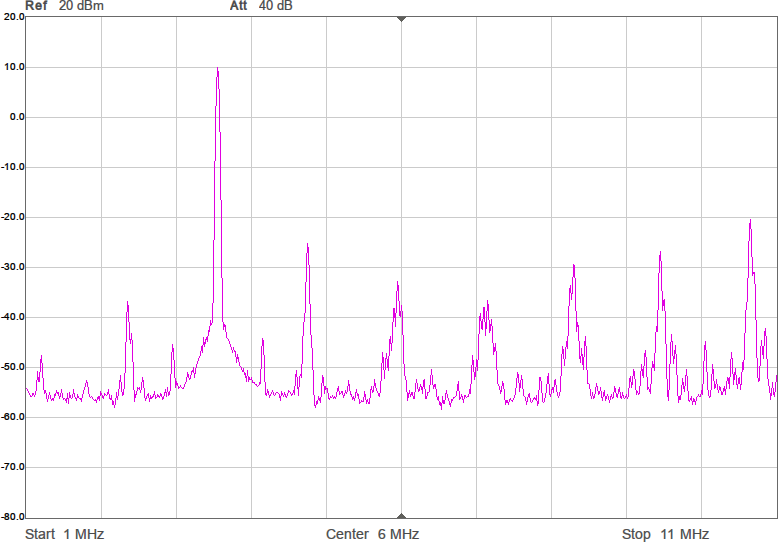
Sagt och gjort. Efter lite (eller ganska mycket…) felsökande fick jag till programkod som räknar ut sigma-delta-modulerade vågformer. Figur 7 visar vågformen och Figur 8 spektrumen med denna metod. Tidigare var HD3 ca 9 dB under grundtonen, men nu är den i värsta fallet ca 20 dB under och i andra fall 30–40 dB under. En hygglig förbättring alltså.

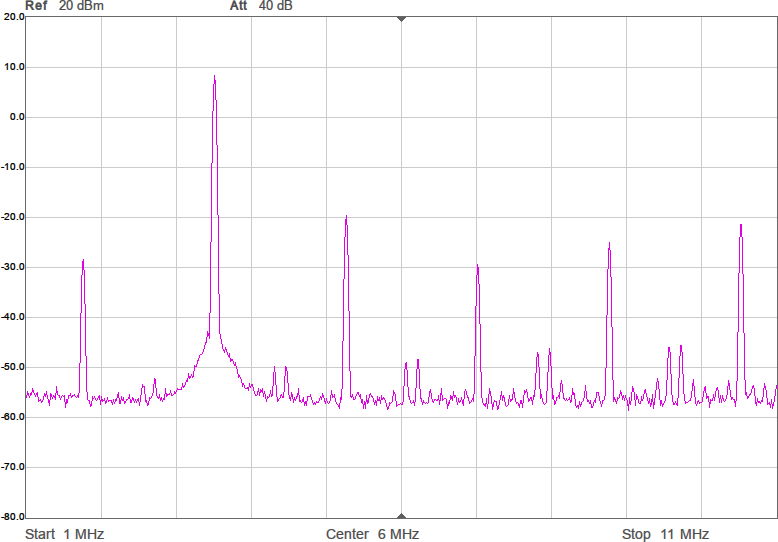
Differentiell utgång

Nu är det väl ändå så bra det kan bli? Vi har ju uppnått väldigt god frekvensupplösning och nedtryckta övertoner, trots att vi bara använder en mikrokontroller utan särskilt stöd för att agera HF-generator. Inte riktigt. Ytterligare en idé jag fick var att använda inte en utgång, utan två, som jobbar i motfas. En fördel med detta är att man kan få ut högre effekt eftersom två utgångar (två ”slutsteg”) hjälps åt. En annan är att man borde undertrycka andra ordningens distorsion som kommer av att pinnarna är olika starka när de driver en hög nivå jämfört med när de driver en låg. En tredje och mindre viktig fördel är att man minskar den högfrekventa strömmen på matningen till processorn eftersom man drar ungefär samma ström hela tiden. Därmed minskar ripplet på processorns matning (vilket i det här fallet knappast är särskilt viktigt).

För att skapa en differentiell signal gäller det att skicka ut en nolla på den ena utgången samtidigt som det skickas ut en etta på den andra och tvärt om. Det kräver dubbelt så mycket förberäknad data eftersom det inte finns något sätt att få en PIO att invertera en signal utan att det tar extra klockcykler. Om man använder samma mängd minne för buffertarna så får man med denna metod alltså bara hälften så många sampel och därmed lite sämre frekvensupplösning. En fin finess är att en PIO kan skicka ut mer än en bit per klockcykel från skiftregistret till olika pinnar. Så genom att lägga udda bitar med omvänd polaritet mot jämna och skriva om PIO-programmet att skicka ut två bitar per klockcykel istället för en så kan man skapa en differentiell signal. Enda ändringen i PIO-programmet är att ettan blir en tvåa för att skifta ut två bitar per klockcykel:

.wrap_target
   out   pins, 2  ; Shift out two bits, one to each pin
.wrap

Vilka pinnar som berörs ställs in i förväg genom registerskrivningar till PIO:n.

En nackdel är alltså att det går åt dubbelt så mycket minne för samma längd på sekvensen och en annan är att DMA:n måste jobba dubbelt så fort, men det är väldigt akademiska invändningar eftersom det ändå finns mer kapacitet i form av minne och DMA-bandbredd än man kan tänkas behöva i den här tillämpningen.

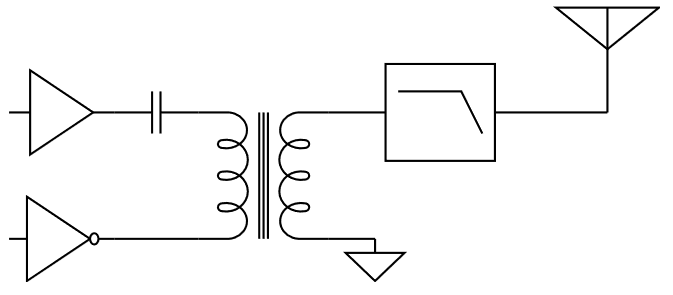
För att skapa signalen till antennen behövs nu en balun, t.ex. i form av en transformator vars primärlindning kopplas mellan pinnarna som drivs i motfas med varandra. En kondensator i serie är också en god idé för att hindra strömrusning om pinnarna av någon anledning skulle sluta ändra nivå hela tiden. Se Figur 9.

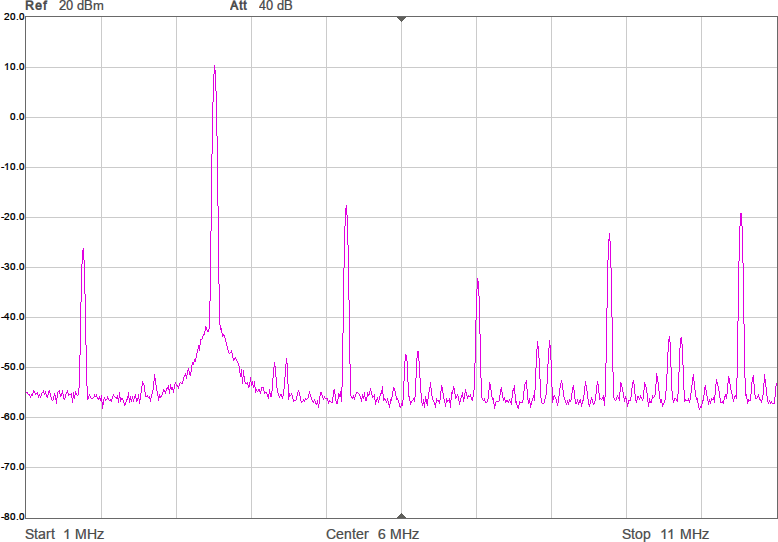
I Figur 10 visas de nya spektrumen. Förutom att signalnivån är någon dB högre har inte mycket hänt. Men man kan notera att HD2 av någon anledning inte blev lägre utan högre i sista spektrumet. Oklart varför.

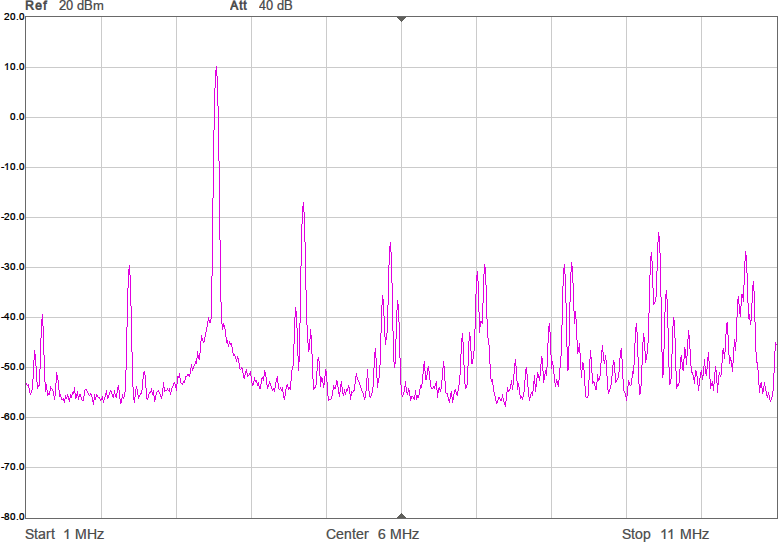
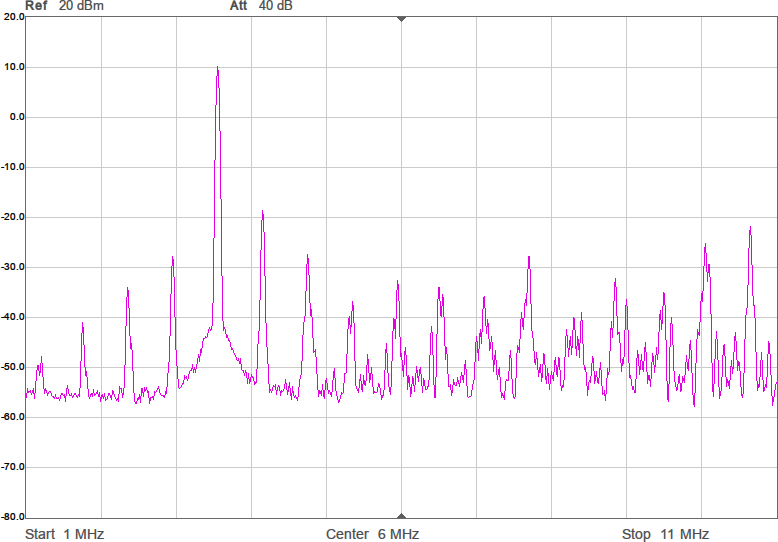
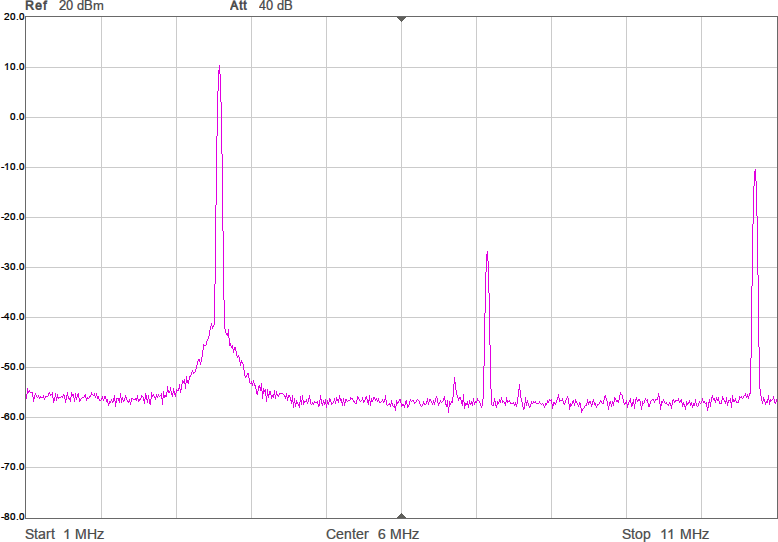
Trenivåers kvantisering

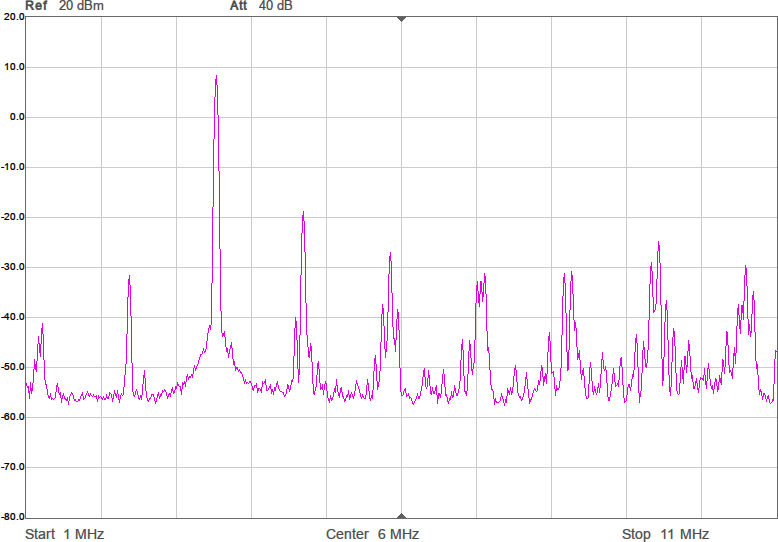
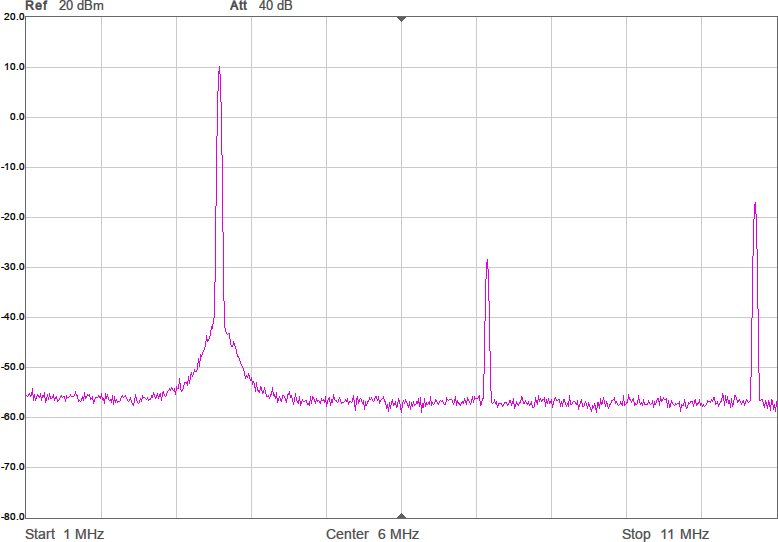
När man har en differentiell signal mellan två digitala utgångar finns det fyra möjligheter; låg-hög och hög-låg har vi utnyttjat, men pinnarna skulle även kunna ha nivåerna låg-låg eller hög-hög. I de två senare fallen blir ju signalen, som är skillnaden mellan utgångarna, noll, men detta är också användbart. Genom att tillåta dessa tillstånd kan vi gå ifrån att kvantisera signalen till ett av två möjliga lägen, som vi kan kalla +1 och -1, till att ha tre nivåer som vi kan kalla +1, 0 och -1. Kvantiseringen blir alltså mindre grov, vilket ytterligare förbättrar spektrumet genom att en del spurioser undertrycks. Figur 11 visar vågformen och Figur 12 spektrumen efter att trenivåers kvantisering införts.

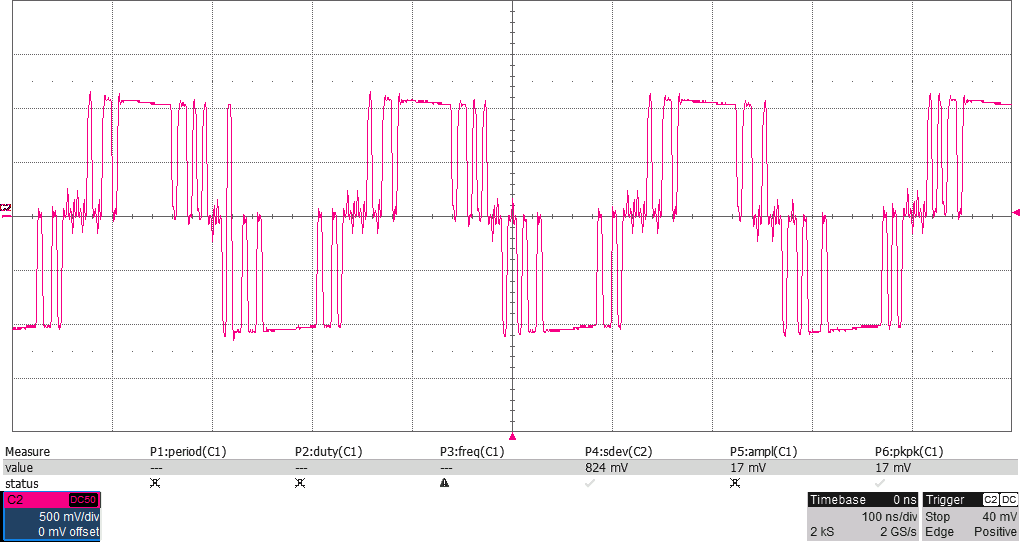
Dithering

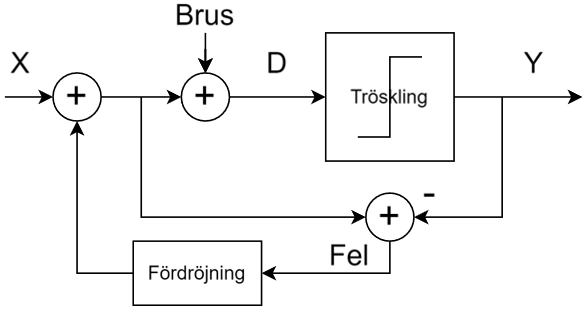
Är vi klara ännu? Nej! Det finns mer att göra. Som synes finns fortfarande ett antal spurioser här och var i spektrumen. Detta är alltså inte övertoner till grundtonen, utan skapas genom en komplicerad interaktion mellan tonen man vill skapa, den begränsade samplingsfrekvensen och kvantiseringen. Skräp som är ihopsamlat till en specifik frekvens är värre än om energin i skräpet vore utspridd över ett bredare frekvensområde eftersom det lättare kan störa ut en smalbandig mottagare. Och spurioser nära grundtonen är svårare att filtrera bort än spurioser på större avstånd. Som tur är finns en teknik att sprida ut dessa toner. Tekniken kallas ”dithering” och går ut på att lägga till brus innan man kvantiserar signalen. Ett blockschema som visar hur detta brus läggs till i sigma-delta-modulatorn visas i Figur 13. Som synes läggs bruset till precis före kvantiseringen och felet som det introducerar fångas alltså upp av den vanliga felåterkopplingen.

Bruset är en serie pseudoslumptal och man kan laborera med hur stora de ska vara samt vilken spektral- och amplitudfördelning de ska ha. En enkel lösning som verkar fungera någorlunda bra är att ha likformigt fördelat brus med samma maxamplitud som på sinusvågen. Spektrum efter tillägget av dithering visas i Figur 14. Som synes har det dykt upp ett brusgolv som blir högre vid högre frekvenser samtidigt som spurioserna sjunkit. Den högsta spuriosen var tidigare den vid ungefär 5,7 MHz vid 3,55 MHz grundton. Nu har denna ton sjunkit med nästan 10 dB.

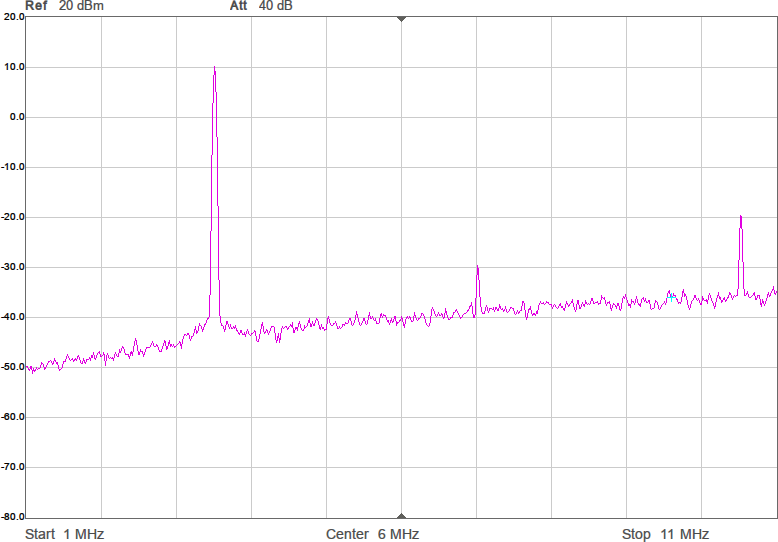
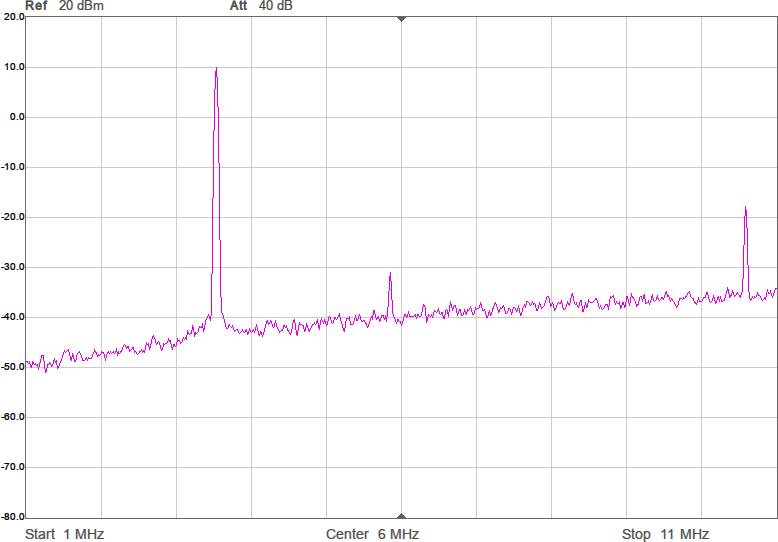
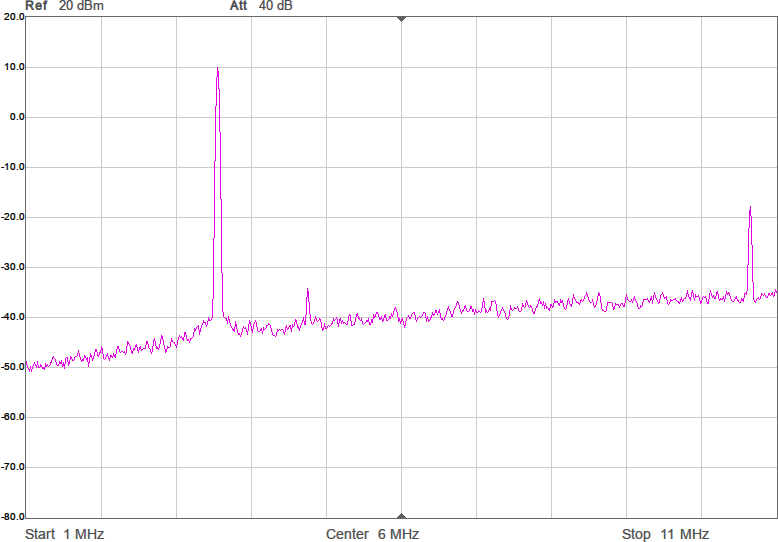
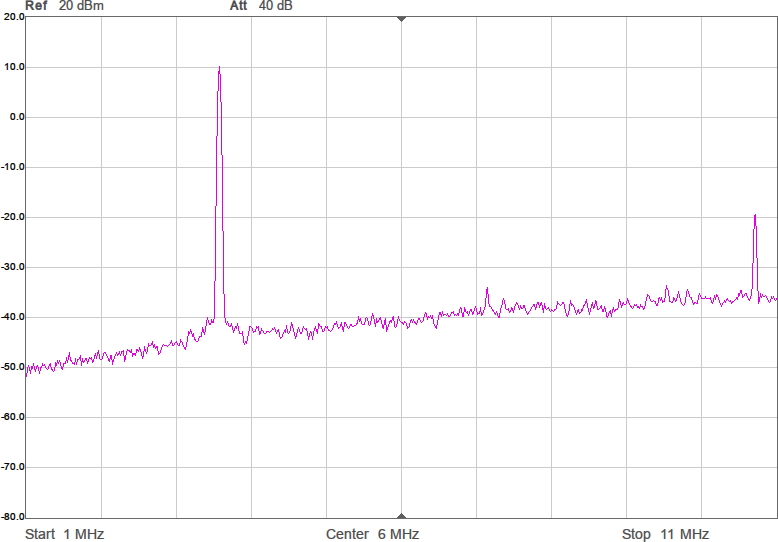
I tidsdomänen ser vågformen lite stökigare ut än tidigare på grund av det pålagda bruset, vilket visas i Figur 15.

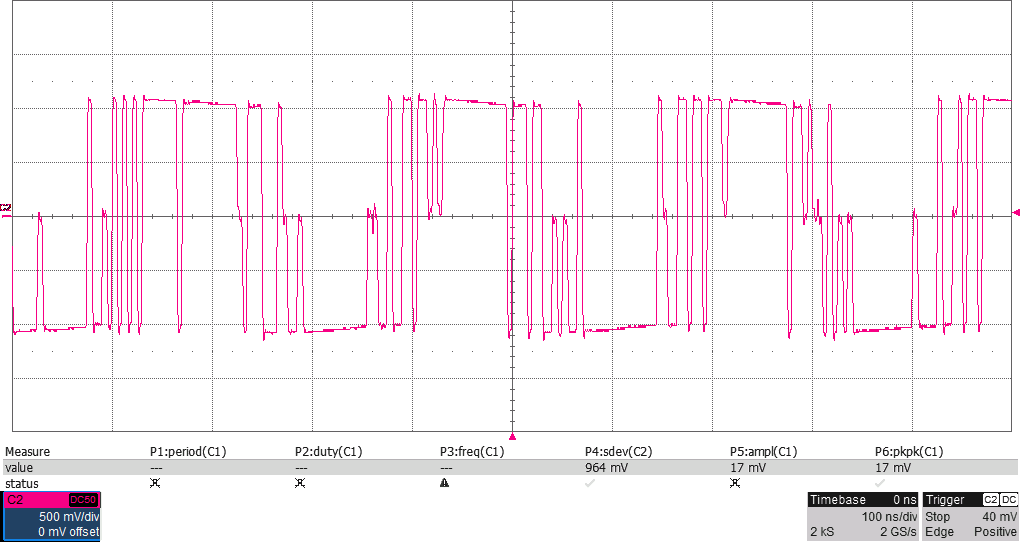
Minskning av nyckelknäppar/splatter

Varför sluta här? En inte så elegant sak med att slå av och på bärvågen abrupt är att man orsakar nyckelknäppar (splatter), dvs skapar störningar i närheten av den frekvens man egentligen har tänkt hålla sig till. Lösningen är att göra övergångarna mellan tystnad och sändning mjukare, dvs att mer gradvis slå av eller på bärvågen. Eftersom vi spelar upp förberäknade vågformer kan vi beräkna sådana som mjukt ordnar en sådan övergång. Det äter upp mer minne och här blir det viktigare att använda tillräckligt långa buffrar för att övergången ska ta tillräckligt lång tid för att väsentligt minska nyckelknäpparna. Föra att inte komplicera programkoden alltför mycket så går vi från att ha en enda buffert med bärvågen till fyra lika långa buffertar för vardera upprampning, bärvåg, nedrampning respektive tystnad. Det går alltså åt fyra gånger så mycket minne (åtta om vi jämför med innan vi gjorde signalen differentiell) och nu börjar vi känna av att minnet trots allt är begränsat.

Liksom tidigare är det DMA som skyfflar data från buffertarna till PIO:n, men eftersom vi nu inte alltid ska upprepa innehållet i samma buffert om och om igen så införs ett interrupt (avbrottsrutin) som anropas varje gång en buffert har spelats färdigt. Om huvudprogrammet som sköter morsesignaleringen exempelvis satt en flagga som säger att det är dags att sluta sända får interruptrutinen styra om så att nästa buffert är nedrampningsbufferten som sedan följs av bufferten med tystnad.

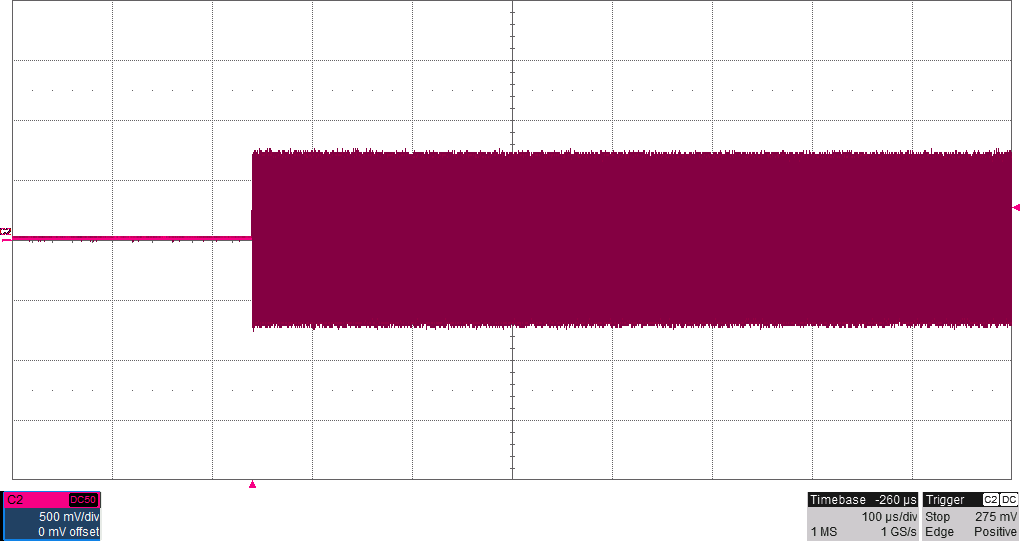
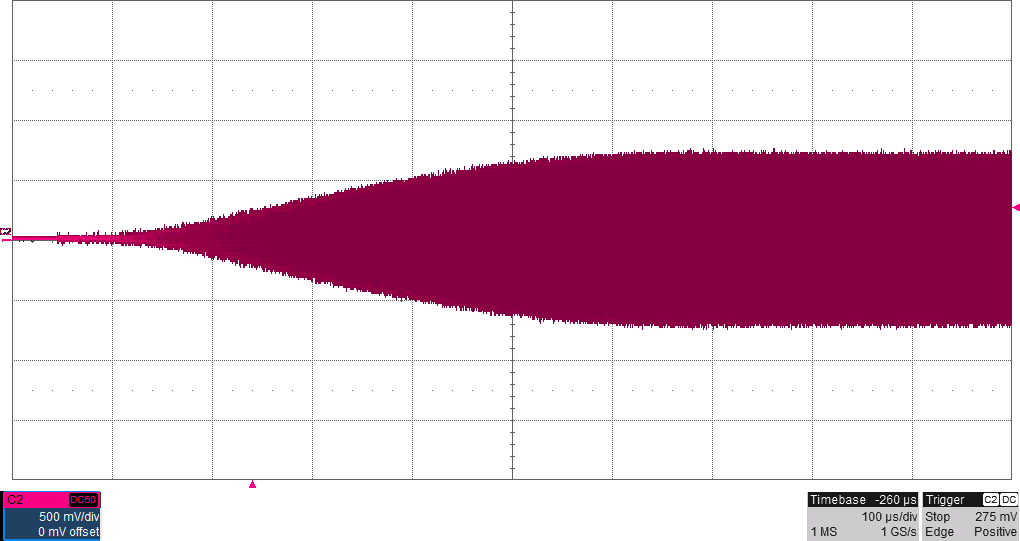
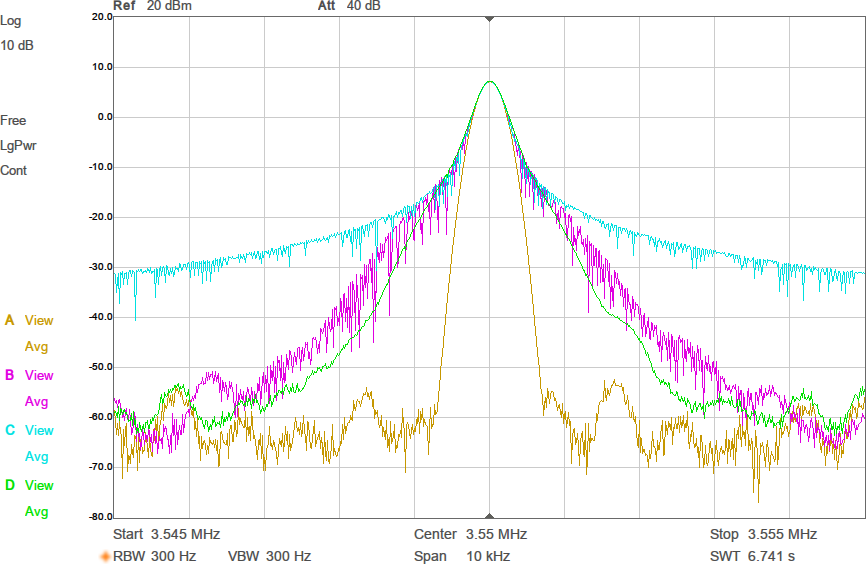
Figur 16 visar hur bärvågen ser ut efter lågpassfiltrering i samband med abrupt respektive mjuk upprampning. I Figur 17 jämförs spektrum mellan konstant bärvåg, mjuka övergångar med 15 000 ord långa buffertar (äter upp nästan allt minne), 10 000 ord långa buffertar, respektive abrupta övergångar. Spektrumen samlades in genom att köra hög morsetakt (många nyckelknäppar per sekund) och använda ”max hold” i spektrumanalysatorn i någon minut för att fånga maximal amplitud vid varje frekvens. Som synes sjunker störningarna i närheten av bärvågen när man har de mjukare ramperna och längre övergångar ger därmed som väntat minskade nyckelknäppar i grannkanalerna.

Byte av processor

Med tanke på de ökade minneskraven kan det vara värt att fundera på att använda den nyare RP2350, monterad på kortet Raspberry Pi Pico 2, som har ungefär dubbelt så mycket minne som RP2040. RP2350 har dessutom inbyggd flyttalsprocessor, så beräkningen av innehållet i buffertarna baserat på frekvens, dithering och nyckelknäppsminimering som tar 16 sekunder på en RP2040 (när buffertlängden är 15 000 ord) minskar till under tre sekunder. En viktigare fördel är att strömförbrukningen är lägre på RP2350. Vid 200 MHz processorklocka och konstant sändning uppmätte jag en minskning av strömmen på 5-V-matningen från 50,5 mA till 38,6 mA när jag bytte till det nyare processorkortet. När sändning inte sker drar Pi Pico 32 mA medan Pi Pico 2 drar 21; återigen vid 200 MHz processorklocka. Det något högre priset på en Pi Pico 2 uppvägs mer än väl av den lägre strömförbrukningen och högre prestandan.

Kod

Den som vill experimentera vidare med metoderna som jag beskrivit i den här artikeln kan ladda ned koden jag skrivit för det hela på [4]. Det är inte kod som är tänkt att användas utan ändringar i en foxoringsändare, utan den erbjuder ett interaktivt sätt att via kommandon man skriver in via ett terminalfönster experimentera med de olika moderna som beskrivits ovan. När strömmen slås på så börjar den snart sända ut signaler som från en foxoringsändare, men det krävs ändringar i koden eller kommandon via serieporten (över USB) för att välja frekvens, kodtakt eller rävnummer.

Del 2

Figur 1 visar en spretig prototyp med RF-delarna som behövs för en sändare. I del 2 av artikeln beskrivs framtagandet av de analoga delarna, bygge på ett riktigt kretskort tillsammans med lite DIP-switchar och en (valfri) display samt komplettering av koden så att det blir en välfungerande foxoringsändare.

Referenser

[1] Online pioasm for Raspberry Pi Pico https://wokwi.com/tools/pioasm

[2] Raspberry Pi Pico Ham Radio Transmitter https://101-things.readthedocs.io/en/latest/ham_transmitter.html

[3] Fast Algorithm for Rational Approximation of Floating Point Numbers https://axotron.se/blog/fast-algorithm-for-rational-approximation-of-floating-point-numbers/

[4] Pi Pico 2 Foxoring transmitter test code. https://github.com/per-magnusson/Foxoring-test-code-for-Pi-Pico-2