So let’s talk some electronics on this blog for a change.
The other day I responded to a forum post about decoupling. Others had responded before me, but I felt that there were room for additional insights. Here is a translation into English of the question and a somewhat extended version of my reply.
Q: It is common to have a decoupling capacitor between power and ground to get a stable supply voltage. In the case of a micro controller the value is typically around 100 nF. My question is: Do I still need the capacitor even at low frequencies (~8 MHz) and when the supply current is rather small, like a few mA at 3 V?
A: The subject of supply decoupling is far more complicated than what has previously been indicated in this discussion thread. But it is not magic.
You might be able to make it work without the capacitor if the circumstances are right and you can most certainly make it fail despite the capacitor if the circumstances are unfavourable.
I do not have the time to write anything remotely complete here and now (others like István Novák, http://www.electrical-integrity.com/ have written thick books about it), but I can try to describe some of the most relevant points for your case.
One good way of thinking about this subject is to realize that the goal is to make sure the impedance of the supply rail (or the Power Distribution Network, PDN, as it is often referred to in the literature) is low enough for all frequencies to prevent too high amplitudes of noise to appear. This observation is more or less trivial, but it is still a good starting point.
So, what impedance do you need and what will you get? My guess is that you have at most two copper layers on your PCB. This is a bad start, but it is quite possible to make slow processors work on such a board anyway. Ideally, you would want to have nice power and ground planes in the PCB with just a thin dielectric layer between them (preferably 0.1 mm or even less) to get a large (well, everything is relative) plane capacitance and a small inductance. This plane capacitance can typically be up to a few nF (a pair of 1 dm^2 planes separated by 0.1 mm of FR4 has a capacitance of 3-4 nF) which probably does not sound too impressive, but it has a very low inductance if the planes are solid and closely spaced and the planes are therefore good at keeping the impedance low at frequencies of maybe 100 MHz and up to a GHz or so. Above a GHz, the inductance of vias and packages makes the planes less relevant and decoupling inside chip packages and on the chips themselves are the only effective decoupling.
If you connect a surface mount decoupling capacitor to the planes and use a good layout with closely spaced vias you will get a parasitic inductance of approximately 1 nH. I have done some research on the inductance of various decoupling layouts and the results can be found here: http://axotron.se/index.php?page=28. The inductance depends not on the capacitance value, but only on the layout and the geometry of the capacitor package, so 1 pF in a 0603 package has the same inductance as 1 µF in the same package.
The parasitic inductance appears in series with the capacitor and forms a resonant circuit (there is also some small series resistance, but we will ignore that for now). See picture below.
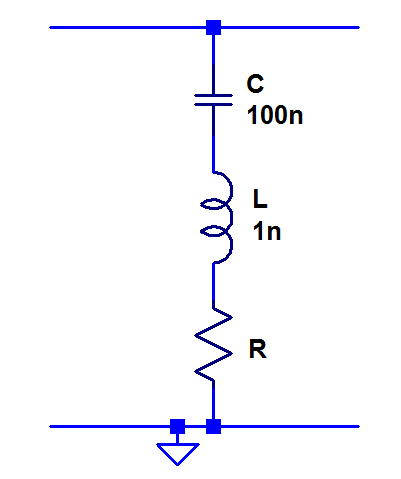
1 nH together with 100 nF results in a resonance frequency of 16 MHz. At this frequency the capacitor is maximally efficient since it has its lowest possible impedance. For frequencies below the resonant frequency, the impedance gradually increases (the capacitance dominates and its impedance increases at lower frequencies) and the same happens above it (the inductance dominates and its impedance increases at higher frequencies). The impedance vs. frequency is plotted below.
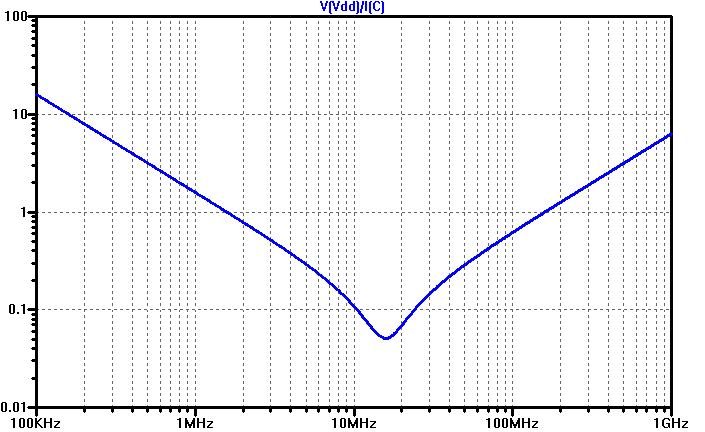
The fact that the capacitor behaves pretty much like an inductor a bit above the resonant frequency does not mean that it is useless at those frequencies. The important thing is that the impedance is kept low enough. The impedance is indeed the same at a tenth of the resonant frequency (where the capacitance dominates) as it is ten times above (where the inductance dominates). So if you are happy with the capacitor impedance at 1.6 MHz (where it is roughly 1 Ω) you might be equally satisfied at 160 MHz (where it has reached 1 Ω once again).
Above 100-200 MHz or so, the planes typically have lower impedance than the decoupling capacitors and if you need low impedance in this range you really need a PCB with properly designed planes.
If you do not have the luxury of power and ground planes, things get worse. The planes are not there to connect the capacitors to the pins of the chip via a negligible inductance and you need to resort to using tracks to distribute the power. A rule of thumb is that a 1 mm long track has an inductance of approximately 0.5 nH (1 nH would be easier to remember and more conservative, but seems to be less accurate for typical PCB tracks). Maybe you are lucky and are using a chip that has power and ground pins next to each other so that you can put a capacitor right at this pin pair to get a decent low-inductance decoupling solution. This might actually work up to a few hundred MHz and if you are lucky again this covers the needs of the chip.
But let’s assume you put a single 100 nF capacitor at the voltage regulator and that it is 10 cm away from the chip. This gives 20 cm of tracks (the inductance in the ground tracks counts as much as the inductance in the power tracks if they have similar geometry) and results in an inductance on the order of 100 nH. This clearly dominates over the inductance of the surface mount capacitor and at 8 MHz (the assumed clock frequency of the processor), this yields an impedance of 5 Ω. If the processor consumes 10 mA at the clock frequency, the ripple is 50 mV, which probably will not cause any trouble for a 3 V digital circuit.
However, the supply current is unlikely to be a sinusoid at the clock frequency. Rather there will be a current spike once per clock cycle and if we assume that the amplitude is 20 mA and that the rise time is 1 ns, we have a time rate of change di/dt of 20 MA/s. This causes a voltage drop over the supply inductance of L*di/dt = 2 V. A ripple of 2 V on a supply of 3 V is not good and is almost guaranteed to cause malfunction. The numbers will be different in each specific case, but the numbers used here are quite realistic and the calculation shows that a few cm of tracks between the decoupling and the chip might be disastrous. If you instead have a board with good planes, the inductance of the planes is so tiny compared to the inductance of the capacitors, so it does not matter much if there are several cm between the decoupling capacitors and the chip.
It is worth pointing out that the above analysis of the current spikes did not assume any particular clock frequency. So it does not matter if they occur once per minute or a hundred million times per second. The resulting noise amplitude will be the same. So the possibly unexpected conclusion is that the switching time (and amplitude) is far more important when it comes to decoupling than the actual clock frequency.
The rise time of outputs is sometimes specified in the datasheets, but then often as maximum values and the interesting thing for decoupling purposes is the minimum rise time. The AC characteristics of the current consumption of the processor itself is rarely, if ever, specified.
In summary, you probably need to use proper decoupling techniques even if the processor is clocked at a relatively low frequency.
There are also more complicated aspects that one might need to consider, but I refrain from going into those in detail here. E.g. if you have several capacitors in parallel, and especially if they have different capacitance and/or inductance, there will be parallel resonances where the impedance peaks, which could cause serious problems. If you have planes, there will also be such a resonance between the capacitance of the planes and the inductance of the decoupling capacitors.
One thing that you should (almost) never do is to put a ferrite or other inductor in series with the supply of a digital circuit. Doing so would add lots of inductance to the supply and thus cause the circuit to much more easily generate a huge amount of ripple on its own supply.