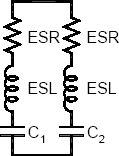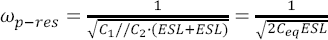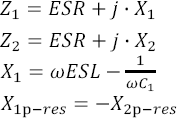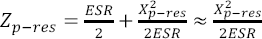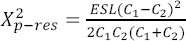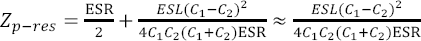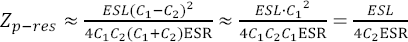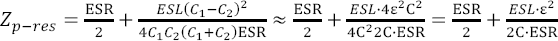Avkoppling

Avkoppling del 3 - Beräkning av resonanser

I föregående avsnitt presenterades ett antal mätningar på olika avkopplingskonfigurationer. I detta avsnitt ska vi försöka skaffa oss lite mer teoretisk insikt genom att räkna på kretsarna.

Men först ett par ord om serie- respektive parallellresonans som redan nämnts några gånger utan närmare förklaring. Med serieresonans menas att de seriekopplade reaktiva elementen i en serie-LCR-krets som i Figur 1 vid någon frekvens får lika belopp men motsatt tecken på sina reaktanser och därmed tar ut varandra. Detta orsakar ett impedansminimum lika med det resistiva elementets resistans. Med parallellresonans menas att de reaktiva elementen i parallellkopplade grenar (som i Figur 13) hamnar i resonans med varandra, vilket orsakar ett minimum i admittansen, dvs. ett maximum i impedansen. Man kan visa att serie- och parallellresonanstoppar alltid kommer omväxlande i kretsar som består av parallellkopplade LCR-länkar. Det ligger alltså alltid en parallellresonanstopp mellan två serieresonanstoppar och vice versa.

Ett fenomen som vi kunde observera i ett par mätningar var att det uppstod parallellresonanstoppar när kondensatorer med olika serieresonansfrekvenser parallellkopplades. Låt oss se om vi kan förutsäga detta med hjälp av lite kretsteori samt försöka dra några slutsatser av resultaten. Beräkningarna är delvis hämtade från [6]. Vi studerar parallellkopplingen av två kondensatorer, med ekvivalent krets enligt Figur 13. För att få rimligt enkla beräkningar som ger någon insikt så har vi satt ESR och ESL lika medan kapacitanserna skiljer sig åt. Som vi tidigare sett kan i verkligheten ESR vara ganska olika om kapacitanserna är olika, men låt oss för tillfället bortse från det för att komma till okomplicerade resultat som ger någon designinsikt.

Parallellresonansfrekvensen blir:

Ekv 3

Där C₁//C₂=C_eq betecknar C₁C₂/(C₁+C₂). Om ESR är lika för kondensatorerna gäller vid parallellresonansen att reaktanserna (X) hos de två kondensatorerna är identiska men har olika tecken:

Ekv 4

En mindre räkneinsats ger att totala impedansen vid parallellresonans är:

Ekv 5

Om ESR är liten kan impedansen vid parallellresonans alltså bli obehagligt stor. Alltför låg ESR är alltså dåligt om man vill undvika höga parallellresonanstoppar. Alltför stor ESR är naturligtvis också olämpligt eftersom det gör att första termen - som försummats vid approximationen i slutet av Ekv 5 - blir stor. Man kan lätt visa att optimum är att ESR är lika med Xp-res, dvs. ESR ska vara lika stor som reaktansen hos den enskilda kondensatorn vid resonansfrekvensen. För keramiska kondensatorer är ESR alltid lägre än optimum och för vanliga elektrolyter är den alltid högre.

Ytterligare lite räknande ger:

Ekv 6

Ekv 7

Som sagt finns det ett optimum för ESR, nämligen X_p-res, och detta optimum blir enligt Ekv 6 lägre (dvs. hamnar närmare det mycket låga ESR som verkliga keramiska kondensatorer har) om:

• ESL är liten,
• C1≈C2 samt
• C1 och C2 är stora.

För att minimera impedansen vid resonansfrekvensen (Zp-res) bör man alltså enligt Ekv 7 hålla ESL låg, C1≈C2 samt C1 och C2 stora. För vanliga keramiska kondensatorer hamnar man dock alltid en bit ifrån optimum och det skulle löna sig att öka ESR (!) om man kunde. Att lägga till ett seriemotstånd kan minska parallellresonanstopparna, men är på det hela taget troligen kontraproduktivt eftersom det kraftigt ökar induktansen och därmed impedansen för alla andra höga frekvenser. Att en relativt hög ESR ger lägre impedans vid parallellresonans beror på att högre ESR sänker Q-värdet på resonanskretsen. Att C1≈C2 ger låg resonanstopp är återigen en anledning till att det är olämpligt att blanda in kondensatorer med onödigt låga värden när man avkopplar.

Två helt olika kondensatorer

Låt oss titta på några specialfall. Vi börjar med två kondensatorer med helt olika värden, dvs. . Om detta sätts in i Ekv 7 får man:

Ekv 8

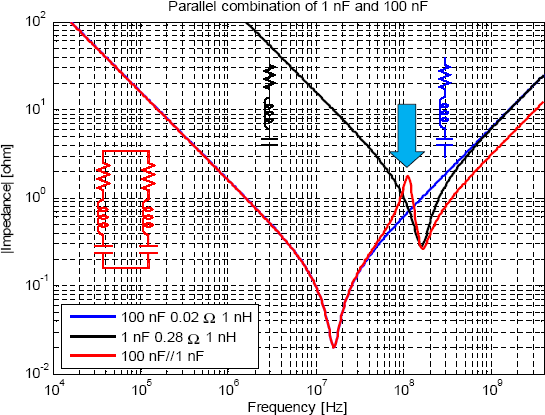
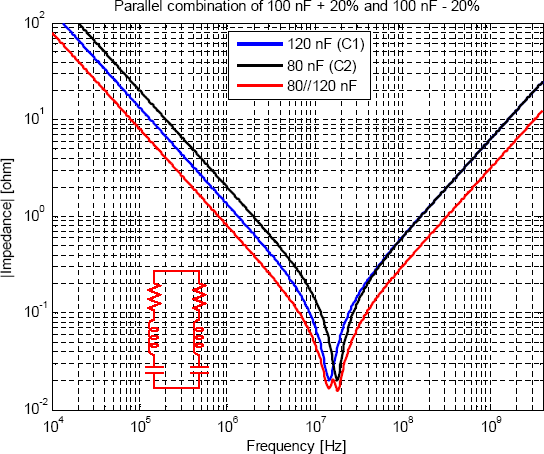
Ekv 8 säger att om man har kondensatorer av liknande typ men med väldigt olika värden parallellkopplade med varandra så ska man minimera ESL, hålla ESR hög och den minsta kondensatorn så stor som möjligt för att inte få en onödigt hög resonanstopp. ESL kan man alltid försöka minimera med en god layout, medan övriga faktorer kan vara svårare att påverka beroende på andra bivillkor. Bäst är förstås att undvika parallellkoppling av kondensatorer med helt olika värden om man inte är tvungen.

Om man parallellkopplar 100 nF 0603 (1 nH, 0,02 Ω) med 1 nF 0603 (1 nH, 0,28 Ω) så är visserligen inte resistanserna lika, men vi kan prova att använda Ekv 8 ändå genom att sätta in medelvärdet av ESR. Formeln förutsäger en resonanstopp på knappt 2 Ω och det stämmer väl med resultatet av en mer detaljerad simulering som visas i Figur 14.

Två snarlika kondensatorer

Om vi istället parallellkopplar två kondensatorer med närliggande värden blir situationen en annan. Låt den ena kondensatorn ha kapacitansen C₁=(1+ε)C och C₂=(1-ε)C. Detta insatt i Ekv 7 ger:

Ekv 9

Ekv 9 säger att om man har kondensatorer med närliggande värden parallellkopplade så är parallellresonanstoppens höjd över ESR/2 proportionell mot kvadraten på avvikelsen från medelvärdet, dvs. den blir väldigt liten om avvikelsen är liten. Det är som vanligt bra att minimera ESL (och öka ESR så länge inte termen ESR/2 börjar dominera) medan stor kapacitans också bidrar till låg resonanstopp. ε²-termen gör att toppen förmodligen är väldigt låg redan från början och därför kan det vara relevant att inte försumma termen ESR/2 i Ekv 9.

Ett realistiskt exempel är två st 100 nF 0603 där den ena har maxtolerans och den andra mintolerans, dvs. den ena har värdet 120 nF och den andra 80 nF. Vidare räknar vi med 1 nH ESL och 0,02 Ω ESR. Här blir resonanstoppen endast 0,02 Ω, dvs. nästan 100 gånger bättre än när 100 nF parallellkopplades med 1 nF. Kurvorna från en simulering visas i Figur 15. Det är alltså inte farligt att parallellkoppla kondensatorer med aningen olika värden, i alla fall inte om parasiterna är snarlika vilket vi förutsatte i härledningen.

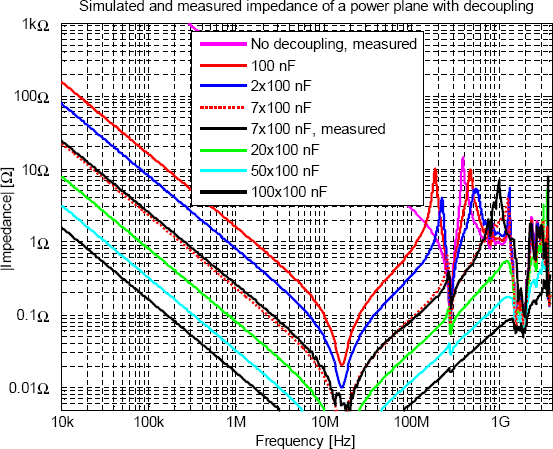
Många kondensatorer med samma värde

Oftast har man många avkopplingskondensatorer och man kan fråga sig hur det påverkar den totala impedansen efter att ha sett att två kondensatorer i vissa fall kan ge upphov till oönskade resonanstoppar. Matematiken blir krånglig om man ska räkna på det för hand, men simulering är lätt och det är möjligt att göra mätningar.

Figur 16 visar simulerad impedans hos ett plan där enbart 100-nF-kondensatorer kopplats in. Planet har modellerats med verkliga mätdata vid beräkningarna. Tre viktiga slutsatser kan dras av simuleringen:

1. Parallellresonanserna blir mindre utpräglade ju fler kondensatorer man använder.
2. Impedansen blir allt bättre (lägre) ju fler kondensatorer som används.
3. Över ca 1 GHz har avkopplingen mycket liten effekt och det är bara planets egen impedans som bidrar som spelar någon roll såvida man inte har extremt många kondensatorer.

Något som inte blir bättre av att man använder fler kondensatorer är kostnaden och möjligen tillförlitligheten, men elektriskt blir allt bättre.

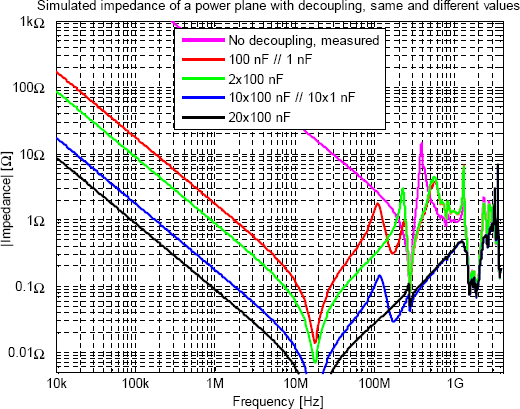
Många kondensatorer med olika värden

Vi kan också simulera skillnaden mellan att bara använda 100 nF samt att ersätta hälften av kondensatorerna med 1 nF. Figur 17 visar resultatet av ett par sådana simuleringar. I ett litet område nära 200 MHz finns en liten positiv effekt av att byta hälften mot 1 nF. Här råkar nämligen 1-nF-kondensatorernas serieresonans hamna nära parallellresonansen och därmed dela upp den på två resonanser med något lägre toppar. Vid i stort sett alla andra frekvenser så blir situationen bara sämre av att byta till lägre värden.

Om man t.ex. av utrymmesskäl är begränsad till ett fåtal kondensatorer skulle man möjligen kunna använda lägre värden för att skjuta prick på frekvenser där man är säker på att man behöver en extra låg impedans. Men för att detta ska vara en god idé måste man verkligen vara säker på sin sak och man måste också mäta upp impedansen hos planet med olika kondensatorvärden monterade för att kunna trimma in det värde som ger serieresonans på rätt frekvens. Utan verifierande mätning är risken stor att man råkar lägga den oundvikliga parallellresonansen som uppstår när olika värden blandas i närheten av den frekvens där man ville ha serieresonansen och då har man förvärrat situationen. I de allra flesta projekt är det i praktiken knappast realistiskt att specialdesigna avkopplingen för vissa frekvenser, utan det är bättre att rikta in sig på att åstadkomma så låg impedans som möjligt över så stora frekvensområden som möjligt samtidigt som man undviker parallellresonanser.

Under dessa förutsättningar är det alltså lämpligt att använda många avkopplingskondensatorer med samma värde i så liten kapsel som möjligt och välja ett så stort värde som man har råd med och kan få tag på i den valda kapseln. Detta är precis vad Howard Johnson förespråkar i [7], medan en del andra författare envist och felaktigt hävdar att det är bra att använda lägre kapacitansvärden än nödvändigt.

Exempel på denna missuppfattning finns i [6] och [8]. Författarna till dessa artiklar har inte insett att storleken på ESL hos olika kapslar är nästan lika stor för t.ex. 0402 som för 0603. Det syns tydligt på att författarna i sina teoretiska impedansplottar visar V-formade kurvor som ligger på samma höjd och bara är förskjutna i frekvensled för kondensatorer med väldigt olika värden. Detta implicerar att de antar att ESL är omvänt proportionell mot kapacitansen, men som vi har visat i bland annat Figur 3 och Tabell 1 är den snarast konstant och oberoende av kapacitansen.

Denna insikt tycks tyvärr inte heller ha nått ut till alla halvledartillverkare. Man kan i datablad ofta läsa rekommendationer i stil med: "Avkoppla Vref med 1 µF parallellt med 100 pF för att få god avkoppling vid både höga och låga frekvenser." Om det nu verkligen behövs två komponenter för att hålla nere impedansen vid höga frekvenser (dvs. induktansen) hade det varit bättre att skriva: "Avkoppla Vref med två stycken 1-µF-kondensatorer i storlek 0402 och minimera ledningslängden mellan kondensatorerna och kretsen." Med denna metod undviker man alltså den höga impedansen vid parallellresonansen mellan kondensatorerna samtidigt som man får lika bra eller bättre egenskaper vid höga frekvenser som man fått om två olika värden använts.

© Per Magnusson