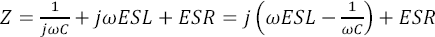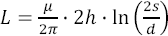|
|
AvkopplingDen här artikelserien är resultatet av ett forskningsarbete som Per Magnusson, Axotron/SP Devices AB, och Gunnar Karlström, BK Development AB, genomfört under 2007 och 2008. Avkoppling del 1 - Bakgrund och kondensatoregenskaperAtt avkoppla matningsspänningar är något man måste göra på så gott som alla kretskort, men trots att det finns avkoppling i nästan alla elektronikkonstruktioner så är det vanligt att konstruktörer inte har så god insikt i hur man ska konstruera avkopplingen för att den ska bli så effektiv som möjligt. Ofta följer man tumregler med tveksam giltighet, kopierar gamla lösningar eller bara chansar. Resultatet blir ibland att det råkar fungera bra, men i en del fall blir lösningen onödigt dyr eller får sämre egenskaper än den skulle kunna ha, t.ex. när det gäller EMC (elektromagnetisk kompatibilitet) eller störningar på interna signaler. I den här artikeln ska vi försöka ge en ökad insikt i hur olika designval man kan göra påverkar egenskaperna hos avkoppling på flerlagerskretskort. Mycket handlar om att förstå vilka parasiter i form av t.ex. induktans som är viktiga i sammanhanget. Förhoppningsvis kan artikeln ta död på några myter och möjliggöra för läsaren att konstruera effektivare och billigare avkopplingslösningar. Innehållet baserar sig till stor del på mätningar utförda med nätverksanalysatorer på ett verkligt kretskort och på enskilda komponenter samt på information från andra artiklar, simuleringar och på teoretiska härledningar. BakgrundDe flesta elektroniska kretsar har en strömförbrukning som varierar mer eller mindre snabbt över tiden. Samtidigt fungerar de bäst om matningsspänningen är konstant. Ohms lag säger att man får en varierande spänning om en varierande ström flyter genom en impedans som är skild från noll, så för att hålla matningsspänningen så konstant som möjligt vill man alltså se till att impedansen hos matningen är låg vid de frekvenser som förekommer i strömförbrukningen. I radiosammanhang kan detta vara i stort sett en enda hög frekvens (plus DC) medan matningsströmmen i digitala kretsar normalt sett är bredbandig och man behöver därför låg impedans i ett mycket brett frekvensområde. Spänningsregulatorer har ofta en bandbredd på sin reglerloop på något tiotal kHz eller mindre och utgångskondensatorerna håller nere utimpedansen i ytterligare någon frekvensdekad. Högre upp i frekvens kan regulatorn inte göra mycket för att hålla spänningen stabil. Ofta har man dock processorer, FPGA:er eller radiokretsar som drar ström med frekvenser på många tiotals eller hundratals MHz eller ännu högre, så ytterligare något måste göras för att förse sådana system med matning av god kvalitet. En bra lösning i många fall är att använda spännings- och jordplan i kortet samt att ansluta ett antal kondensatorer mellan dessa för att hålla nere impedansen vid höga frekvenser så att den högfrekventa strömförbrukningen inte ger upphov till alltför stora spänningsvariationer. Hur effektiv avkopplingen blir beror bland annat på planens utformning, vilka kondensatorer som används och hur dessa kondensatorer kopplas in. Impedansen hos en verklig kondensatorI detta avsnitt ska vi lägga grunden till förståelsen av avkopplingens beteende vid höga frekvenser genom att studera beteendet hos en enskild avkopplingskondensator mer i detalj. Impedansen hos en ideal kapacitans minskar linjärt med ökad frekvens och avkopplingskondensatorer borde därför ge låg impedans vid höga frekvenser, precis som man vill. Tyvärr beter sig inte verkliga kondensatorer som ideala kapacitanser för alla frekvenser som är av intresse. Vid någon frekvens börjar parasitisk induktans (ESL, ekvivalent serieinduktans) i serie med kondensatorerna spela roll. Impedansen hos en induktans stiger linjärt med frekvensen, så när väl serieinduktansen har börjat dominera så blir kondensatorns avkopplande verkan allt sämre ju högre upp i frekvens man går. Oundvikligen finns det även en viss resistans (ESR, ekvivalent serieresistans) i serie med verkliga kondensatorer och en viss parallellresistans (läckresistans) parallellt med den. Parallellresistansen är dock ovidkommande i avkopplingssammanhang, så den ignorerar vi. Vår sammantagna modell för en avkopplingskondensator med parasiter visas i Figur 1.
Figur 1. Modell av verklig avkopplingskondensator.
Impedansen är summan av impedanserna hos elementen i modellen:
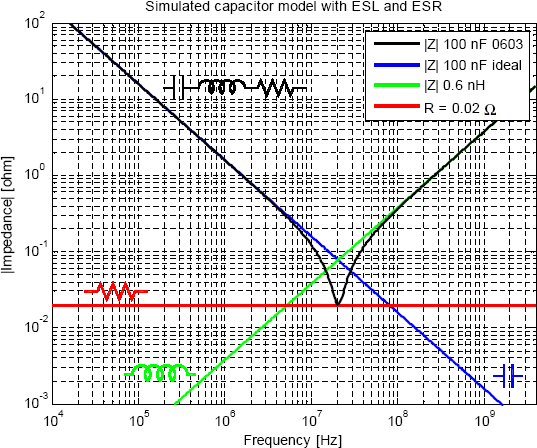
Där vinkelfrekvensen ω=2πf har använts för att förenkla formlerna något. För att få en hållpunkt i verkligheten kan vi ta en vanlig 100-nF-kondensator med dielektrikum X7R i 0603-kapsel. Enligt Murata [1] har en sådan kondensator en ESR på ca 0,02 Ω och en ESL på ca 0,6 nH. Det innebär att reaktanserna hos kapacitansen och serieinduktansen har samma belopp och tar ut varandra vid ca 20 MHz. Denna frekvens är kondensatorns resonansfrekvens och här blir totala impedansen helt reell och lika med ESR = 0,02 Ω. Över resonansfrekvensen dominerar reaktansen från induktansen och den totala impedansen stiger linjärt med frekvensen. Figur 2 visar beloppet av impedansen hos denna kondensator samt de olika delkomponenterna i modellen som funktion av frekvens.
Figur 2. Simulerad impedans hos en 100-nF-kondensator
samt impedansen hos de olika delarna i modellen.
Det kan kanske förvåna att självresonansfrekvensen (SRF) hos kondensatorn är så pass låg eftersom man brukar använda 100 nF 0603 för att avkoppla kort med frekvenser långt över 20 MHz. Dessbättre är vi i avkopplingssammanhang inte beroende av att kondensatorn beter sig som en perfekt kapacitans, utan det räcker med att impedansen är låg, vilket den är långt över resonansfrekvensen. Vid 10×SRF = 200 MHz är t.ex. impedansen densamma som vid SRF/10 = 2 MHz, så om vi har samma impedanskrav vid båda dessa frekvenser är vår 100-nF-kondensator alltså lika bra i båda fallen. Hur som helst så är den lilla serieinduktansen i kondensatorn helt avgörande för beteendet vid frekvenser över SRF. Avvikelsen mellan den blå linjen (ideal kapacitans) och den svarta i Figur 2 är som synes avsevärd. Om vi tittar på parasiterna hos ytterligare några verkliga kondensatorer så finner vi att ESL är i stort sett oberoende av kapacitansvärde om vi håller oss i samma kapsel. En 0603-kondensator har alltså samma ESL oavsett om kapacitansen är 1 pF eller 10 µF. Detta är en mycket viktig observation och leder som vi ska se till slutsatsen att vi inte har något att vinna impedansmässigt (möjligen kostnadsmässigt) på att använda oss av lägre kapacitansvärden om vi håller oss i samma kapsel. Ett lägre kapacitansvärde, exempelvis 10 nF istället för 100 nF ger 10 gånger högre impedans under resonansfrekvensen och i och med att ESL är samma för de två komponenterna så kommer impedanserna en bit ovanför resonans att vara identiska. Visserligen har 10-nF-kondensatorn en högre resonansfrekvens, men det är bara precis runt sin resonansfrekvens som den har lägre impedans än 100-nF-kondensatorn. ESR är normalt sett högre för kondensatorer med lägre kapacitans (i samma kapsel). Om man går till mindre kapslar, t.ex. 0402, så minskar ESL en aning. Det är alltså bättre ur avkopplingssynpunkt att välja kondensatorer med mindre kapsel. Skillnaden är dock inte dramatisk och kan lätt dränkas i ströinduktans från en mindre lyckad layout. Tabell 1 visar data för några relevanta kondensatorer.
Tabell 1. Data för några kondensatorer, enligt Murata
[1].
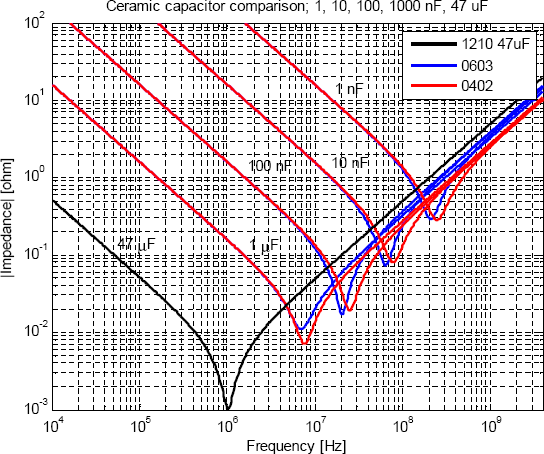
Figur 3 visar impedans som funktion av frekvens för kondensatorerna i Tabell 1. Notera särskilt hur impedansen hos en kondensator med lägre värde är högre än impedansen hos en med högre värde vid i stort sett alla frekvenser.
Figur 3. Simulerad impedans som funktion av frekvens för ett antal olika keramiska kondensatorer.
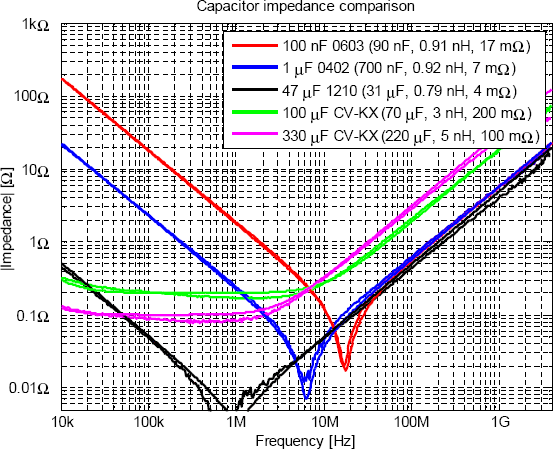
En välspridd myt är att lägre kapacitansvärden ger bättre avkoppling vid höga frekvenser. Detta stämmer precis runt SRF hos den mindre kondensatorn, men i övrigt ligger det inget i myten så länge man håller sig till samma kapsel. Värt att notera är även att skillnaden mellan 0603 och 0402 inte är särskilt stor. Det exakta värdet hos ESL är svårt att mäta och påverkas av mätmetoden. Howard Johnson har t.ex. mätt på uppskalade modeller av avkopplingskondensatorer [5] och kommit fram till lägre värden än vad som anges av Murata. Övriga parasiterDet är inte bara parasiterna i själva komponenterna som spelar roll, utan även parasiter på kortet. Kondensatorerna ska som bekant anslutas till planen och detta sker genom kopparmönster och vior. Främst bidrar layouten med ytterligare induktans. Om man gör en bra layout för en avkopplingskondensator så sitter viorna som ansluter den till planen mycket nära lödytorna, och det är därmed induktansen i viorna som dominerar vid sidan om induktansen i själva komponenten. En approximativ formel för induktansen hos ett par av vior ges i [2] och den lyder (efter konvertering till metriska enheter):
Där h är viornas längd, d är deras diameter och s centrumavståndet mellan dem. µ är permeabiliteten i vakuum och µ/(2π) = 2×10-7 H/m. Eftersom avståndet och diametern står innanför logaritmen så är induktansen alltså ganska svagt beroende av dessa, medan den beror linjärt på viornas längd. Vill man hålla nere induktansen ska man alltså ha kort avstånd i kortet mellan avkopplingskondensatorerna och de plan de avkopplar samt minimera avståndet mellan viorna och i den mån det är möjligt ha stor håldiameter. Som oftast när det gäller formler för induktans så är denna formel inte exakt och det finns ett antal antaganden man gjort för att förenkla matematiken, bland annat att hela magnetfältet från viorna ligger instängt mellan två plan, vilket inte är sant för den del av viorna som sticker upp ovanför planen. Dock ger formeln en fingervisning om hur olika parametrar påverkar induktansen samt ungefär hur stor den blir. Figur 4 visar några olika tänkbara layouter. De tre alternativen till vänster har onödigt hög induktans på grund av olämplig placering av viorna medan de två senare är bra layouter med låg induktans. Speciellt om spännings- och jordplanen ligger långt från den sida av kortet där kondensatorn är monterad kan det löna sig att ha mer än en via per lödyta.
Figur 4. Layouter för avkopplingskondensator. De tre första
rekommenderas ej eftersom induktansen är onödigt hög, medan resten har
låg induktans.
Låt oss använda Ekv 2 för att beräkna hur mycket induktans som viorna bidrar med i en typisk layout. Om vi antar att kortet är 1,6 mm tjockt och spännings- och jordplanen är symmetriskt placerade nära mitten i kortet så blir h = 0,8 mm. Vidare antar vi en håldiameter på 0,3 mm och ett centrumavstånd mellan viorna på 1 mm. Detta ger en induktans på 0,6 nH. Totalt får man därmed en induktans på ca 1,2 nH för 0603 och 1,0 nH för 0402, och man kan notera att den relativa skillnaden mellan 0603 och 0402 minskar ytterligare om man tar hänsyn till parasiter i layouten eftersom de parasiterna inte nödvändigtvis minskar för att man byter kapseltyp. Howard Johnson mäter i [3] upp en minskning av induktansen på ca 20-50% när viorna placeras som i Figur 4 jämfört med om de placeras i förlängningen av kondensatorn. Om man har plats kan man lägga fler vior runt avkopplingskondensatorernas lödytor för att få ner totala induktansen hos avkopplingen och på så vis minska impedansen vid höga frekvenser ytterligare utan att behöva kosta på sig fler kondensatorer. Detta visas i högra delen av Figur 4. Efter 2-3 vior per lödyta avtar dock vinsten eftersom kondensatorns ESL börjar dominera allt mer. Att lägga till fler vior lönar sig ännu mer om man använder lite mer exotiska kondensatorkapslar som 0306 eller 0508 där anslutningsterminalerna ligger längs komponentens långsidor istället för längs kortsidorna. Denna typ av kapsel har radikalt mindre ESL än vanliga avkopplingskondensatorer (ner mot 0,05 - 0,15 nH enligt [1]) och för att dra nytta av det behöver man många vior. En stor nackdel med sådana kondensatorer är dock pris och tillgänglighet, men har man behov av extremt bra prestanda så kan de vara ett alternativ. Något man ska undvika om man vid höga frekvenser vill få valuta för pengarna man lägger ut på avkopplingskondensatorer är att låta flera kondensatorer dela på samma par av vior. Gör man det kommer inte induktansen att vara nämnvärt mindre med två kondensatorer än med bara en eftersom via-induktansen inte minskar när den extra kondensatorn läggs till. Ett specialfall där man trots allt med fördel kan låta två kondensatorer dela på ett via-par är när kondensatorerna sitter på motstående sidor av kortet. Då går nämligen strömmen genom de två kondensatorerna i olika delar av viorna och parasitinduktanserna hamnar därmed parallellt, vilket ger upphov till lägre impedans. Om man inte placerar viorna mycket nära lödytorna blir naturligtvis induktansen hos ledarna mellan kondensatorn och viorna också signifikant. En fingervisning om hur mycket det rör sig om är att varje mm ledning tillför ca 0,5 nH. Glöm inte att räkna med längden på ledningen till vardera lödytan. Att beräkna induktansen som tillförs av spännings- och jordplanen för en kondensator som sitter en bit ifrån störkällan är inte helt enkelt. I [3] hävdas att induktansen ligger i storleksordningen 0,005 nH/mm, men några närmare förutsättningar som t.ex. avstånd mellan planen anges inte, så man kan inte ta det som en universell sanning även om det kanske ger en aning om storleksordningen. Howard Johnson argumenterar i [4] för att man kan beräkna den extra induktansen orsakad av planen mellan en avkopplingskondensator och en mätpunkt (t.ex. en krets som ska avkopplas) genom att använda Ekv 2 på via-paret som bildas av ena vian vid kondensatorn och ena vian vid mätpunkten där h är avståndet mellan planen. Här är antagandet att magnetfälten från viorna helt innesluts mellan planen mer korrekt än i exemplet ovan där formeln användes, men det är kanske inte uppenbart att planen själva inte bidrar med någon signifikant induktans. Tabell 2 visar induktansen enligt denna formel för några tänkbara dimensioner.
Tabell 2. Induktans orsakad av avståndet mellan
kondensator och mätpunkt enligt Ekv 2.
Att tiodubbla avståndet mellan mätpunkt och avkoppling ökar alltså induktansen med ca 0,19 nH, medan en dubblering av avståndet mellan planen också dubblerar induktansen. Detta illustrerar dels att det är fördelaktigt att ha så litet avstånd mellan planen som möjligt och dels att avkopplingskondensatorer som sitter en signifikant bit bort från en viss krets ändå bidrar till att avkoppla kretsen. En mycket viktig slutsats är att induktansen man inför om man har en extra mm ledare mellan en avkopplingskondensator och dess vior (ca 0,5 nH/mm enligt tumregeln) kan vara betydligt större än induktansen som införs om man ökar avståndet mellan kretsen och kondensatorn med 10 mm. Det lönar sig alltså betydligt mer att fokusera på att minska induktansen mellan varje kondensator och planen än att försöka placera kondensatorerna nära kretsarna som ska avkopplas. ElektrolytkondensatorerSom avkoppling i frekvensområdet mellan spänningsregulatorns bandbredd och det område där de keramiska avkopplingskondensatorerna är effektiva passar ibland elektrolytkondensatorer bra. Den här artikeln behandlar främst avkoppling vid högre frekvenser, så endast ett mycket begränsat urval elektrolytkondensatorer har undersökts. Tabell 3 visar egenskaperna hos ett par kondensatorer ur Sanyos CV-KX-serie av lågimpedanselektrolyter. ESL anges sällan eller aldrig av elektrolyttillverkarna, så de värden som finns i tabellen är uppmätta med nätverksanalysator. Man kan notera att uppmätt ESR är ungefär hälften av vad tillverkaren lovar som max, men man kan förvänta sig att ESR ökar vid lägre temperaturer och när kondensatorn åldras, så de låga värdena är inte direkt förvånande. Elektrolyter skiljer sig från keramer genom att ESR dominerar i ett brett område runt resonansfrekvensen eftersom ESR är så hög relativt reaktansen hos kapacitansen och ESL vid resonansfrekvensen.
Tabell 3. Egenskaper hos ett par
elektrolytkondensatorer av lågimpedanstyp.
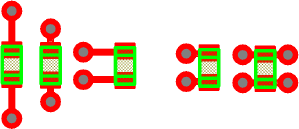
Figur 5 är en jämförelse mellan uppmätt och simulerad kapacitans hos några olika kondensatorer. De komponentvärden som använts vid simuleringen har anpassats för att ge kurvor som överensstämmer så väl som möjligt med de uppmätta kurvorna. Värt att notera är att alla kondensatorerna håller lägre kapacitans än nominellt, trots att ingen DC-förspänning låg över dem vid mätningen. Man kan undra om kondensatortillverkarna kanske har väldigt god kontroll över kapacitansen och utnyttjar detta samt de stora angivna toleranserna (±20 % eller mer) till att alltid ligga i undre delen av toleransintervallet. Mätningarna gjordes med nätverksanalysator med en fixtur där kondensatorn shuntade en transmissionsledning. S21-parametern räknades sedan om till impedans. De uppmätta induktanserna hos både 0603 och 0402 är högre än vad som anges i [1], vilket antagligen beror på skillnader i mätmetod. Förmodligen ger den fixtur vi använde lite för höga värden på ESL, åtminstone för små komponenter.
Figur 5. Uppmätt och simulerad impedans hos några
olika kondensatorer. De taggigare kurvorna är uppmätta.
© Per Magnusson |
| Senast uppdaterad: 2016-12-11, 14:28:06 |
|

![[SW flag]](pic/Sw_flag_40.png)
![[UK/US flag]](pic/UK-US_flag_40.png)